Chordal Graph: Simplicial vertex
なんか意外に反響があった(アクセスログを見ていたらみんなが見ていてくれた)のでやる気を出したのと,少し今回の内容が簡単だったのもあって が〜っと書いてしまいました.2回目のChordal Graph回です. 今回は次回にやる予定のPerfect elimination orderingのための準備として, Simplicial vertexについて説明していこうかと思います.
Simplicial vertexとは
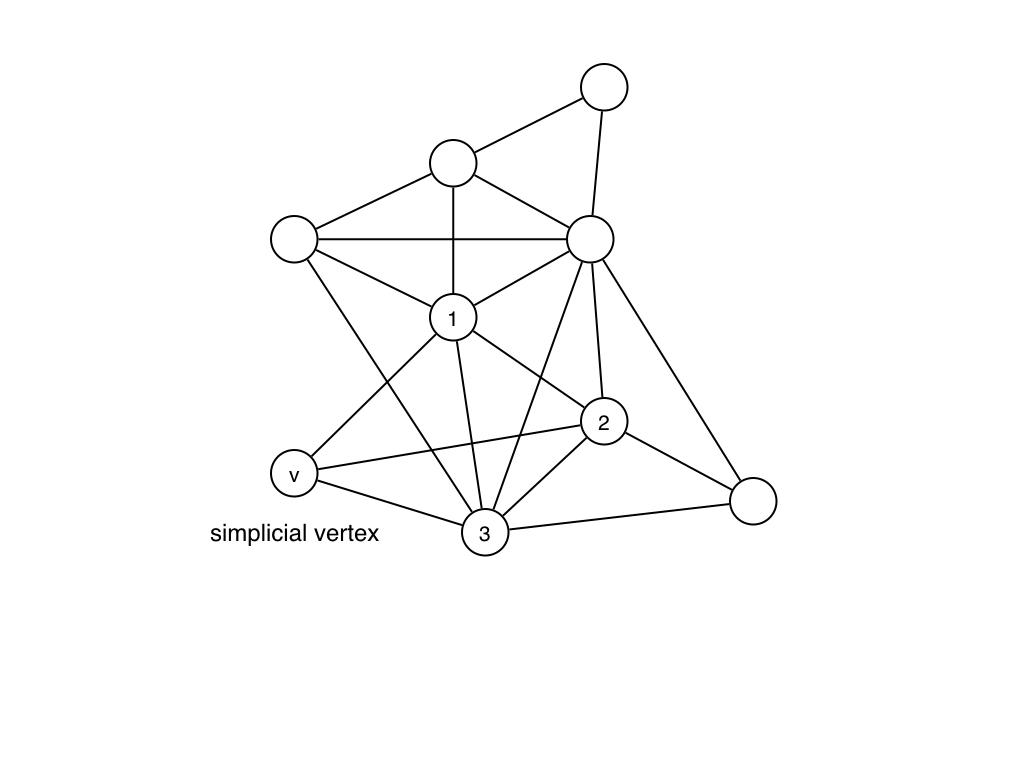
Simplicial vertexとはすごく単純で,グラフ$G$中で$G[N[v]]$がcliqueになる頂点$v$のことです. 図に書くとこんな感じですね.($N[v]$は$v$の隣接頂点と$v$からなる集合を表します.) 下の図では頂点$v$は隣接頂点$1, 2, 3$がclicqueになっているのでsimplicial vertexになります.
さあ,これがchordal graphとどういう関係があるのかというと,次の定理が知られています.
$G$がchordal graph,かつcomplete graphではない. $\to$ $G$は少なくとも2つの隣接しないSimplicial vertexを持つ
以前紹介した定理よりは少し直感的に正しそうな定理ですね(個人的な感想). それでは証明していきます.
今回は頂点数に関する数学的帰納法で証明します. 頂点数$2$の場合はグラフは2つしかなくて,頂点$u, v$間に辺がある場合とない場合の2つのグラフしかありません. 辺があるとcomplete graph,辺がない場合は$u$と$v$がsimplicial vertexなので,この定理は成り立ちます. なので,頂点数$k$のchordal かつ completeでない全てのグラフは定理を満たすと仮定します. なので,頂点数$k + 1$の任意のchordal かつ completeでないグラフ$G$を考えます. $G$中の隣接しない2頂点$u, v$を取ってきて,その2頂点をseparateするminimal separatorを$S$とします. このとき,$G$がchordalなので,$S$はcliqueになります.(前回の記事に証明があります) さらに,$S$がseparatorなので,連結成分$A$と$B$が$G \setminus S$中に存在します. ここで,$u \in A$,$v \in B$としても一般性を失わないのでそう仮定します. したがって,$A \neq \emptyset$かつ$B \neq \emptyset$となります. $G[A \cup S]$と$G[B \cup S]$を考えると,この2つは$\size{G[A \cup S]}, \size{G[B \cup S]} < \size{G}$を満たします.
$G$の誘導部分グラフはchordalなので,$G[A \cup S]$と$G[B \cup S]$がcompleteでないならば, 帰納法の仮定より,simplicial vertexを2つずつ持つことになります. さらに,$G[A \cup S]$中のsimplicial vertexを2頂点$x, y$とすると, $x, y$は隣接しません.したがって,$x$か$y$のどちらかは$S$に含まれていません. なぜなら$S$はcliqueだからです.ここで,$S$に含まれる頂点を$x$とします. すると,$y$は$A$に含まれ,$G[A \cup S]$中の$y$の隣接関係と $G$中の$y$の隣接関係は一致します. したがって,$y$は$G$中でもsimplicial vertexになっています. また,$G[A \cup S]$と$G[B \cup S]$がcompleteだったとしても, それらのグラフは$S$に含まれないsimlicial vertexは必ず1つは持ち, その2つの頂点は元のグラフで隣接していないので,$G$は隣接していない2つのslimlicial vertexを持ちます. よって証明終了です. 証明のイメージ図はこんな感じですね.

$G$を2つに分割するんですが,そうすると$G$よりサイズの小さい2つのグラフができて,その2つのグラフはchordalだし,たとえcompleteだとしても1つは $S$に含まれないsimplicial vertexを持つので,隣接しない2つのsimplicial vertexはあるよね!という証明です. ただし,図中の$x$のように分割後の$G[A \cup S]$や$G[B \cup S]$中でsimplicialだとしても元のグラフ$G$ではsimlicialではない頂点もあります. そういう頂点を考慮しても隣接しない2つのsimplicial vertexがchordal graph$G$中には存在します.
今回の内容は少し軽めでしたが,
すみません,以前の証明は間違いがありました.
現在は修正されています.(11/06)
この定理はこれからの証明にすごく便利なので, 僕としては後になればなるほどいい性質だなぁと感心しました.
Chordal Graph: Minimal vertex separators
chocobaby-aporo.hatenablog.com
Chordal Graph回の第一回目です.今回はMinimal vertex separatorsを紹介します.
Minimal vertex separators
まず,$G = (V, E)$中の頂点集合$S \subseteq V$が,vertex separator (separator)とは 次のような2頂点$u, v$が存在することを言います.
- $u, v$は$G$中の連結成分に含まれるが,$G \setminus S$では同じ連結成分に含まれない.
この時,$S$は$u, v$をseparateすると言います.
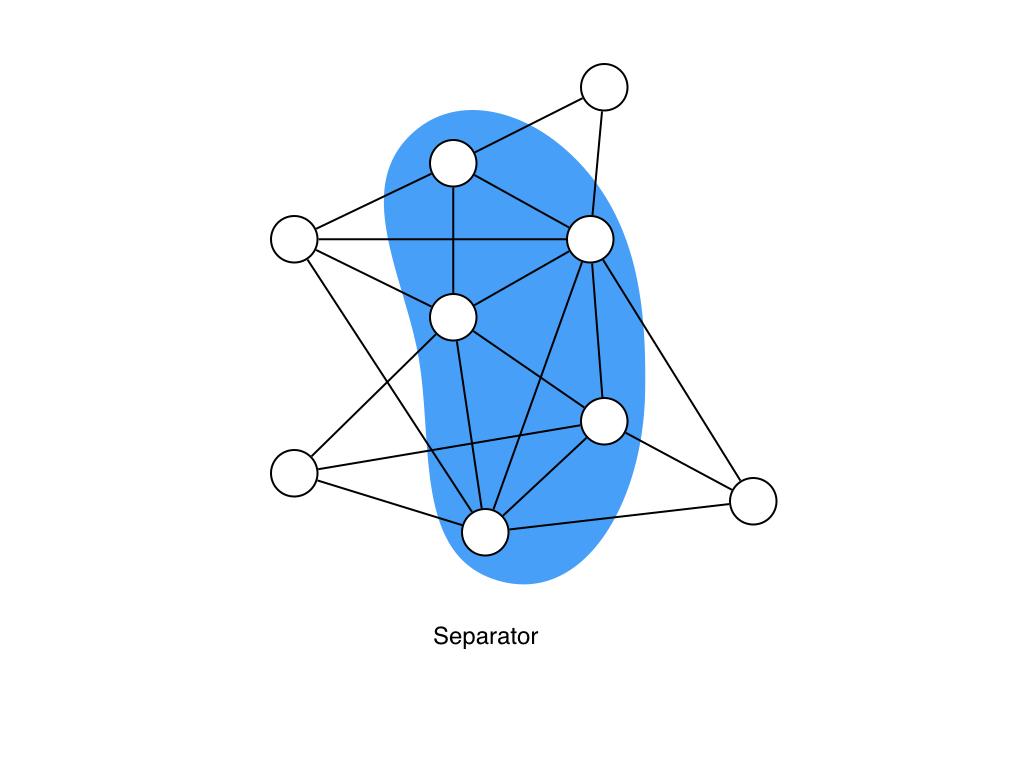
簡単にいうと下の図のような頂点集合です.一応この例のグラフはchordalになっているはずです.
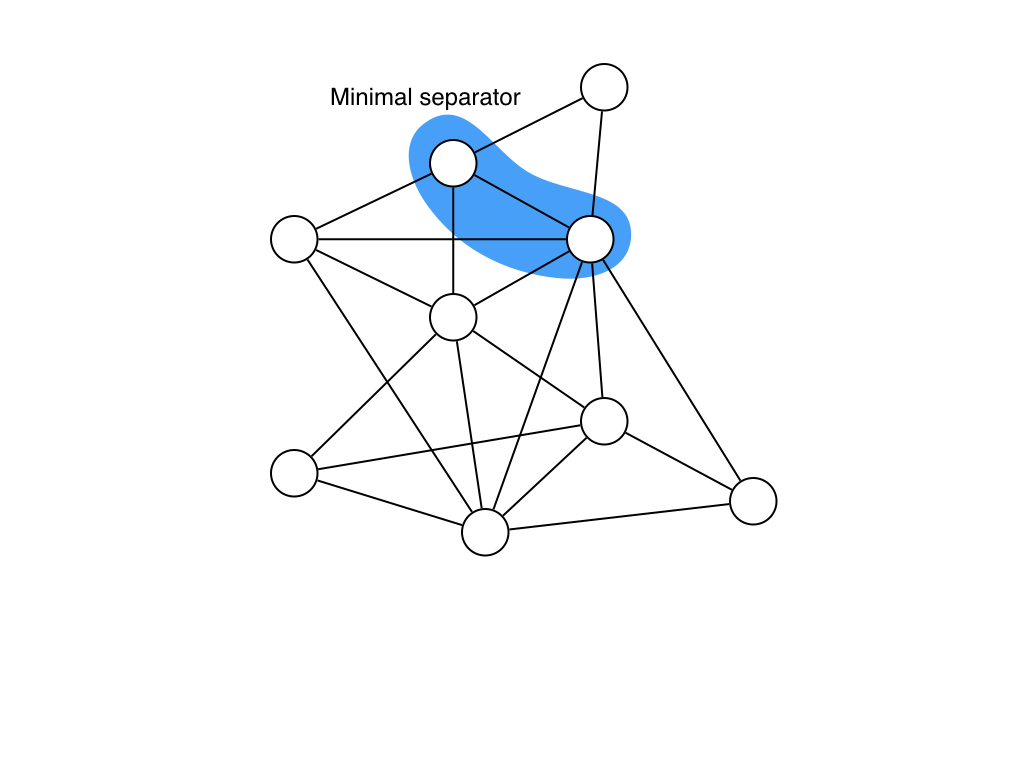
 特に,Minimal separatorというとSeparatorの中でもどんな頂点を除いてもseparator出なくなるようなseparatorです.
特に,Minimal separatorというとSeparatorの中でもどんな頂点を除いてもseparator出なくなるようなseparatorです.
ここでChordal Graphの面白い性質1つ目ですが,次のような定理が知られています.
グラフ$G$がchordalである. $\iff$ $G$中の全てのminmal separatorがcliqueである.
$G$がchordalであるという条件を$A$,$G$中の全てのminmal separatorがcliqueであるという条件を$B$とします. まず$\lnot A \to \lnot B$,つまり$B \to A$について証明します. $G$がchordalではないので誘導部分サイクル(誘導部分グラフかつサイクル,要は弦を含まないサイクル)$C = (u_1, \dots, u_k)$が存在します.$(k \ge 4)$. この$C$中の隣接しない2頂点$u, v$をseparateするMinimal separatorを$S$とすると,この$S$は$C$中の隣接しない2頂点を含むのでcliqueではありません. したがって$B \to A$が成り立ちます.
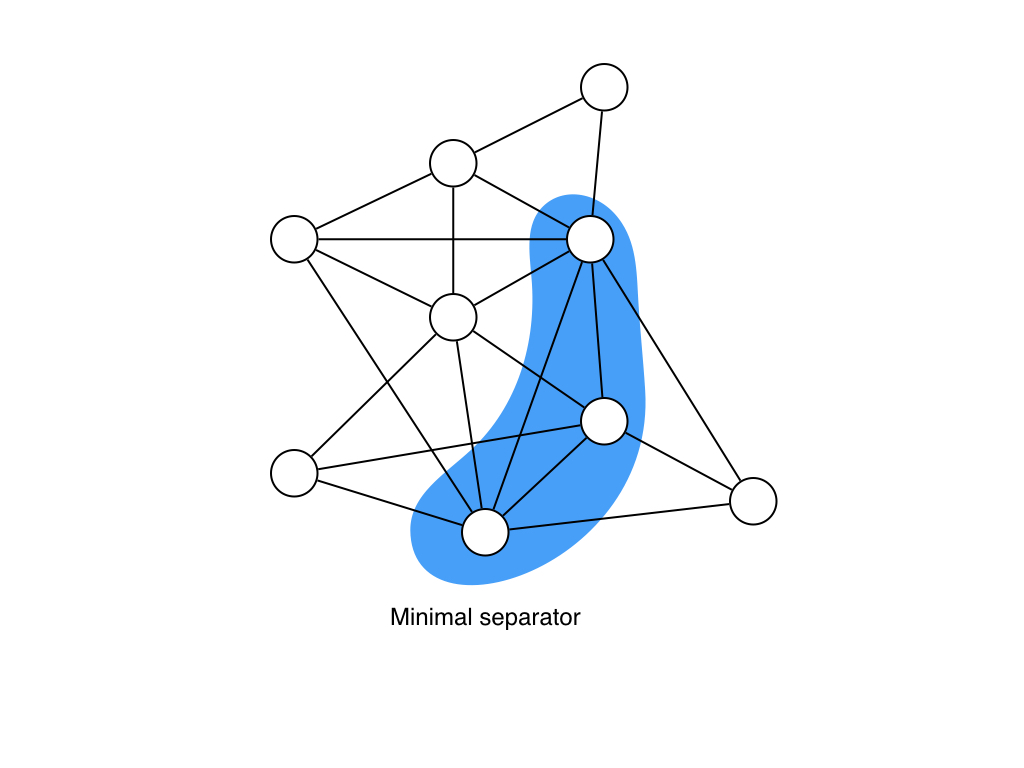
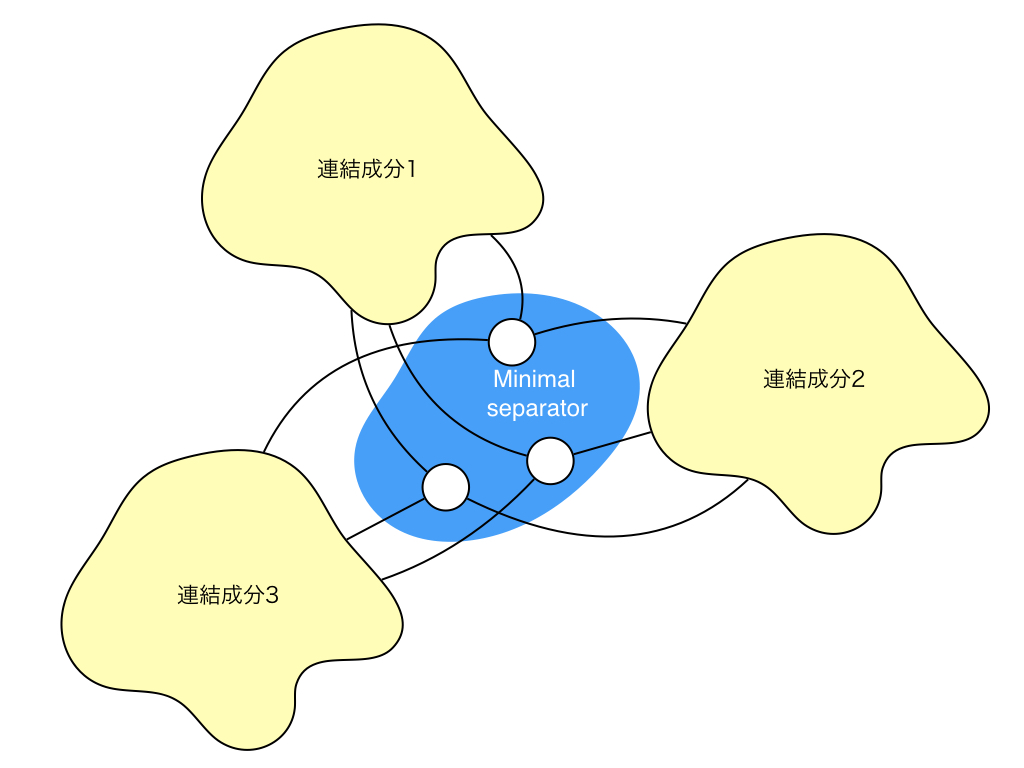
次に$A \to B$を証明します. $S$を任意のminimal separatorとして,$G \setminus S$の連結成分の集合を$\sig C$とします. ここで重要なこととして,minimal separator $S$中の任意の頂点$u$は必ず$\sig C$中のすべての連結成分と隣接しています. もし全ての隣接成分と隣接していない頂点があると,minimal性が成り立たないからです.図で見るとこんな感じの状態になっています.
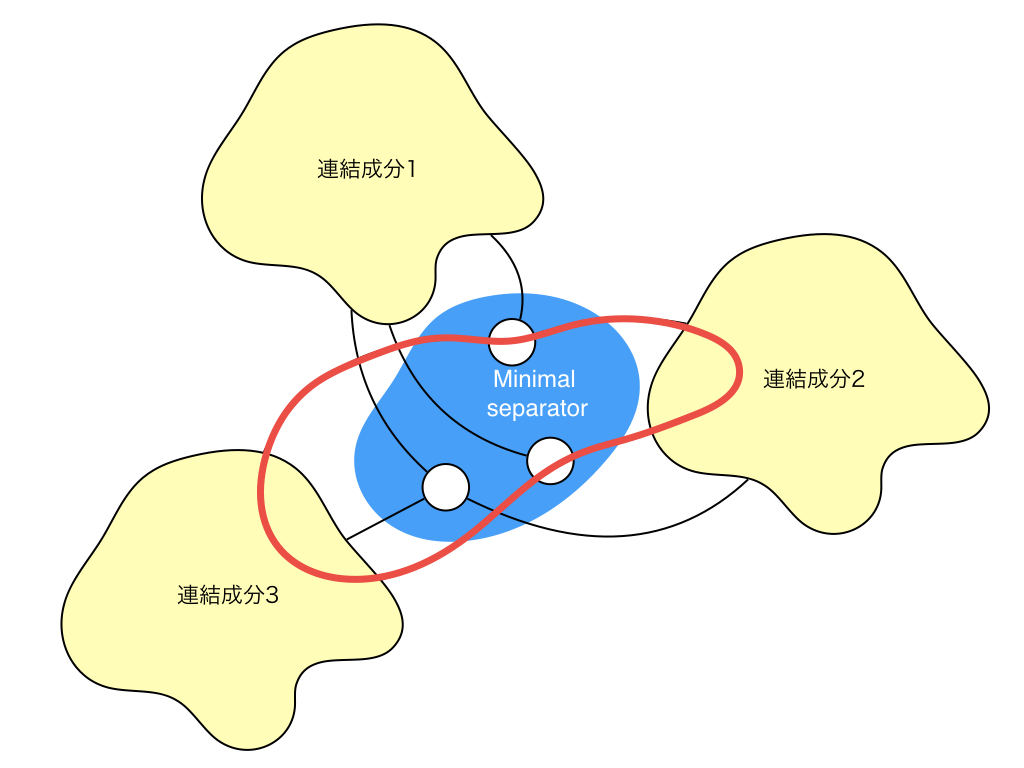
ここで,この性質から$S$中の任意の2頂点$u, v$は$G$中のあるサイクルに含まれることがわかります. しかも,そのサイクルの中には$S \setminus \set{u, v}$中の頂点を含まないサイクルも存在します. (要は$S$中の要素の$u$と$v$だけを含むサイクル)図中の赤線がそのサイクルを表しています. このサイクルは必ず長さが4以上なので,このサイクル中には必ず弦があります. この弦が$u, v$を結ぶ弦なら$u, v$は隣接するし,もし$u, v$を結ばないならその弦を含む$C$より短いサイクルができるため, 最終的には$u, v$を含む長さ4のサイクル$C'$ができます.ここで,$G$がchordalなので, $C'$も弦を含むのですが,$u$と$v$以外のサイクル中の頂点,つまり異なる連結成分同士の頂点を結ぶと,$S$がseparatorであることに矛盾するので, $u$と$v$を結ぶしかありません.つまり$S$中の任意の2頂点$u, v$は隣接しています.言い換えると$S$が誘導する$G $の誘導部分グラフ$G[S]$はcliqueになります.
まとめ
というわけで,Chordal Graphの面白い性質その1は
- グラフ$G$がchordalである. $\iff$ $G$中の全てのminmal separatorがcliqueである.
という性質でした.正直Choralの定義だけみて,「それなら全てのminimal separatorはcliqueになるのか〜」と気付く人はほとんどいないと思いますが, こんな面白い性質があることが知られています. まだまだ面白い性質があるので,気合が続く限り紹介していきます.
追記
今はまだ事実だけを書いておきますが,実はMinimal separatorの数はchordal graphの頂点数よりも少なくなることが知られています. それについての論文が出ていて,これですね. chordal graph以外でもminimal separatorの数については研究されています. あまり僕が理解していないので申し訳ないですが,一般のグラフでのMinimal separatorの数は O(1.6181n) なので, chordal graphではminimal separatorの数がすごく少なくなるのが知られています. 一般のグラフでのMinimal separatorの数の上限についてはここを参照してください.
Chordal Graph
最近Chordal Graphがマイブームです. このシリーズの記事でわからないところやこれ間違っているぞっというのがあったら Twitterで教えてくれると僕が喜びます.
- Twitter ID: kazu0x17
Chordal Graphとは
Chordal Graphとは任意の長さ4以上のサイクルに対して弦が存在するグラフです.wikiへのリンク ここで,ある辺$e$がサイクル$C = (u_1, \dots, u_k)$の弦(chord)とは,$e = \set{u_i, u_j}$かつ,$e$が$C$に含まれない辺のことです. つまり,$C$をより短いサイクルにする辺ということですね.こんな感じの例です.

これだけ聞くと,なんの感想もわかないのですが,実は色々と面白い性質があって最近勉強中です. この記事のネタ本はこれです. これから何回かに分けて自分の勉強を兼ねてこの本の内容を紹介をしていこうと思います.
とりあえず紹介しようかと思っている内容のキーワード
- Minimal vertex separators
- Perfect elimination ordering (PEO)
- Maximum cardinality search (MCS)
- Lexicographical breadth first search (Lex BFS)
- Potential maximal clique
- Simplicial vertex
- Clique tree
- Tree width
- Cops and Robber game
CodeFestival2016本戦の問題
この前Code Festival2016に行ってきました.問題はこんな感じでした.
- A問題 Where's sunuke まあ,A問題なのでやるだけ問題です.
#include<iostream> using namespace std; int main(){ int h, w; std::cin >> h >> w; string s; for (int i = 0; i < h; i++) { for (int j = 0; j < w; j++) { std::cin >> s; if(s == "snuke"){ std::cout << (char)(j + 'A') << i + 1 << std::endl; } } } return 0; }
- B問題Exactly N points
どうせB問題もやるだけだろうと思って適当に貪欲解を投げたらWAでびっくり.一応一瞬考えたらにぶたんでできそうだけど,B問題でにぶたんが出るわけないと思い,貪欲解を適当にいじって2回提出してもなおWA.しょうがないからにぶたん書いてACしました.(B問題でにぶたんが出るようになったんだなぁ)
#include<iostream> using namespace std; bool check(int n, int maxi){ for (int i = maxi; i > 0; i--) { if(n >= i){ n -= i; } } return (n == 0); } int main(){ int n; std::cin >> n; int l = 0, r = n, mid = (r + l)/2; while(r - l > 1){ if(check(n, mid)){ r = mid; }else{ l = mid; } mid = (l + r)/2; } for (int i = r; i > 0; i--) { if(n >= i){ std::cout << i << std::endl; n -= i; } } return 0; }
- C問題Interpretation
$M$種類の言語があり,$N$人の人がいます.それぞれの人が喋れる言語が与えられるので任意の人が喋れるかどうかを判定しろという問題です.通訳を頼んでもいいのである人AとBが共通に喋れる言語がなくても,AともBとも喋れるCさんがいればOKという問題です.
これは$N + M$のサイズの二部グラフ作って,グラフの連結性を判定すれば良いので結構簡単.
#include<iostream> #include<vector> using namespace std; void dfs(vector<vector<int> > &g, vector<bool> &used, int v = 0){ used[v] = true; for (int i = 0; i < g[v].size(); i++) { if(used[g[v][i]] == true)continue; dfs(g, used, g[v][i]); } } int main(){ int n, m, k; std::cin >> n >> m; vector<vector<int> > l(n + m); for (int i = 0; i < n; i++) { std::cin >> k; for (int j = 0; j < k; j++) { int tmp; std::cin >> tmp; l[i].emplace_back(tmp - 1 + n); l[tmp - 1 + n].emplace_back(i); } } vector<bool> used(n + m, false); dfs(l, used); bool flag = true; for (int i = 0; i < n; i++) { flag &= used[i]; } std::cout << ((flag == true)?"YES":"NO") << std::endl; return 0; }
- D問題 Pair Cards
この辺から結構難しく感じました.ある種の最大マッチング問題としても解けるけど,一般のグラフの最大マッチングは頂点数$N$に対して,$N^{2.5}$が最速だったと思うので,どう考えても無理.(しかも1,2時間で実装できるわけがない).なので,制限されたグラフクラスのマッチングなのかと思い,グラフを書いてたりしてたら,整数の和が$M$になるようなペアを作りたいので,与えられた整数を$M$でmodをとって,その値が同じなら同じ整数と考えてもいいことに気づく.なので,後は$M$でmodとった値が$i$の整数と$M- i$の整数をペアにしていけばいいことがわかる.ただし,まだ同じ整数のペアの数は考慮できていないので,この方法でペアを作って,余った整数で同じ整数があったらそのカード同士をペアにする必要がある.
#include<iostream> #include<vector> #include<set> using namespace std; int main(){ int n, m, maxi = 0; std::cin >> n >> m; vector<int> x(n); for (int i = 0; i < n; i++) { std::cin >> x[i]; maxi = max(maxi, x[i]); } vector<int> mod(m, 0); for (int i = 0; i < n; i++) { mod[x[i]%m]++; } int ans = 0, tmp; for (int i = 1; 2*i <= m; i++) { if(2*i == m){ tmp = mod[m/2]/2; ans += tmp; mod[m/2] -= tmp*2; }else{ tmp = min(mod[i], mod[m - i]); ans += tmp; mod[i] -= tmp; mod[m - i] -= tmp; } } tmp = mod[0]/2; ans += tmp; mod[0] -= tmp*2; vector<int> s(maxi, 0); for (int i = 0; i < n; i++) { s[x[i]]++; if(s[x[i]] >= 2 and mod[x[i]%m] >= 2){ s[x[i]] -= 2; mod[x[i]%m] -= 2; ans++; } } std::cout << ans << std::endl; return 0; }
- E問題Cookies
この問題はコンテスト中は部分点しか取れなかったです.制約を見て,dpなら部分点は取れると思い,dpの方針で考えてました.考えたいたdpは「ちょうど$k$枚のクッキーを焼くのにかかる時間は何分か?」というdpを考えました.コードはこんな感じです.
#include<iostream> #include<vector> #include<cmath> using namespace std; typedef long long int lli; int main(){ lli n, a; std::cin >> n >> a; vector<lli> cost(n + 1, 1e9); cost[0] = 0; cost[1] = 1; for (lli i = 2; i <= n; i++) { cost[i] = min(cost[i], (lli)i); for (lli j = 2*i; j <= n; j+=i) { cost[j] = min(cost[j], cost[i] + j/i + a); } } lli ans = n; for (int i = 1; i <= n; i++) { ans = min(ans, (lli)(ceil(n/double(i)) + cost[i] + a)); } std::cout << ans << std::endl; return 0; }
とりあえずこれで$O(N log N)$にはなっているとおもいます(計算量解析はあまりきちんと考えていないけど多分あっている気がする.)コンテスト中はここまでしかわかりませんでした.
コンテスト後,解説を見ながら「頭いいなぁ」と感心しながらコードを書いて次のコードでACしました.コードがpythonなのはC++でオーバーフローを機にするのが面倒だったのでpythonで書きました.
#!/usr/bin/env python # -*- coding: utf-8 -*- def pow(a, b): if b == 1:return a if b%2 == 0: return pow(a*a, int(b/2)) return a*pow(a*a, int(b/2)) def binaryOne(n, multi): l, r = 0, n mid = (l + r)/2 while r - l > 1: if pow(mid, multi) >= n: r = mid else: l = mid mid = (r + l)/2 return r; def binaryTwo(n, maxi, multi): l, r = 0, multi mid = (l + r)/2 while r - l > 1: if pow(maxi, (multi - mid))*pow(maxi - 1, mid) >= n: l = mid else: r = mid mid = (r + l)/2; return l n, a = map(int,raw_input().split(" ")) ans = 1e18 for i in xrange(0, 40): maxi = binaryOne(n, i + 1); subt = binaryTwo(n, maxi, i + 1) ans = min(ans, a*i + maxi*(i + 1) - subt) print ans
今年もパーカーをゲットできたので非常に良かったです.今年はパーカーラインが去年より高めで,半分くらいの人しかパーカーをもらってなかったぽいです.
ビームスタックサーチ
この前,ビームサーチを書いてみたので,今度はビームスタックサーチを書いてみました.この辺のサイトを参考に勉強しました.
このサイトに載っているchokudaiさんのスライドが(ビームサーチをわかっている人なら)結構わかりやすいと思いました.ビームスタックサーチは僕なりの理解として,ビーム幅を増やしながら何回もビームサーチを行うのだが,今までのサーチ中で探索したノードを記憶しておいて,一度探索した部分は探索しないようにしているようなビームサーチという感じです.ビームサーチで厄介(らしい)ビーム幅の設定を色々頑張らなくとも,探索時間をこちらで設定すればその時間内で,頑張れるだけ勝手にビーム幅を増やしてくれるので,楽ができるという利点があるようです.
解いた問題はナップサック問題で,計算時間を2秒で設定して計算しました.コードはこんな感じです.
確かにビームスタックサーチの方が計算時間を設定できる分使いやすそうだという印象でした.
Code Festival 2016に参加しました
今年もCode Festivalを開催していただけて(しかも,本戦まで行けて)本当に楽しかったです.問題セットも良問ぞろいでした.下の方に今回解いた問題セットがあるのですが,どのコンテストでも1問以上はこの問題考えた人頭いいなと思う問題があってすごかったです.結果は220人中98位だったのでかなりいい感じかと思います.しかも,今回はいつも負けている人に初めて勝つことができたのがいい記念になりました.(しかもきちんとパーカーもゲットした).実は問題文を読んですらいない問題や,制約見てできそうだけどよくわからんといって投げた問題が結構あるので,後で解いて自分なりの解説をしてみたいです.問題セットはこんな感じでした.
今年は壇上で表彰されたいなぁとかひそかにに思ってたので,一番可能性たかそうなcsenryuにbrute force attackしてみたけど,DEGwerさんに大賞を取られてしまったのはちょっと悲しい.
初めての機械学習
なんやかんやあって初めて機械学習のアルゴリズムを実装しました.機械学習アルゴリズムの実装といっても大したことなくて,PRLMという教科書の最初にある多項式フィッティングというものを実装してみました.点が$N$点与えられるので誤差関数$E(\vec{w})$を最小化する$M$次多項式求めるというアルゴリズムです(入力は$N$個の点$x$と,整数$M$,出力はベクトル$\vec{w}$).誤差関数$E(w)$は次の二乗誤差の関数を使いました.
- $E(\vec{w}) = \Sigma_{n = 1}^{N} (y(x_n, w) - t_n)^{2}$
解説は次のページがわかりやすかったです.(僕が読んだ教科書と同じ教科書を読んで解説記事を書いていてくれたので,)
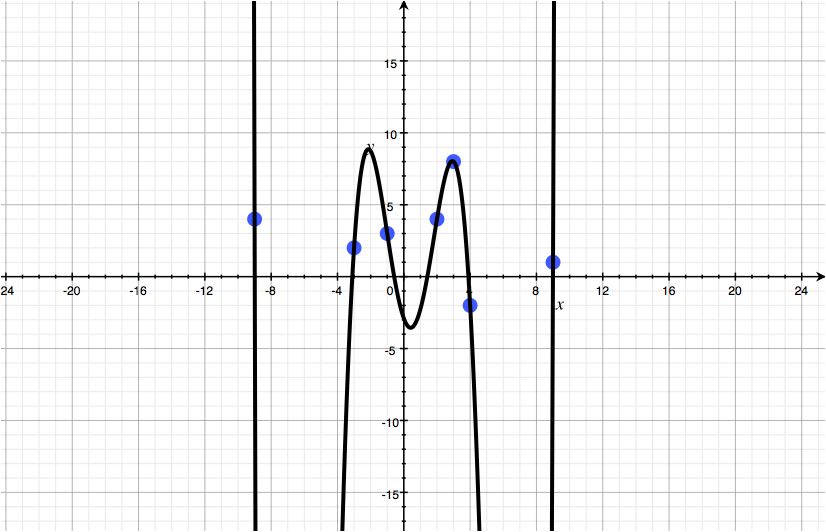
点(2 4), (9 1) ,(3 8), (-1 3) (4 -2) (-3 2) (-9 4)で,
$M = 7$の場合
 $M = 5$の場合
$M = 5$の場合
 $M = 3$の場合
$M = 3$の場合
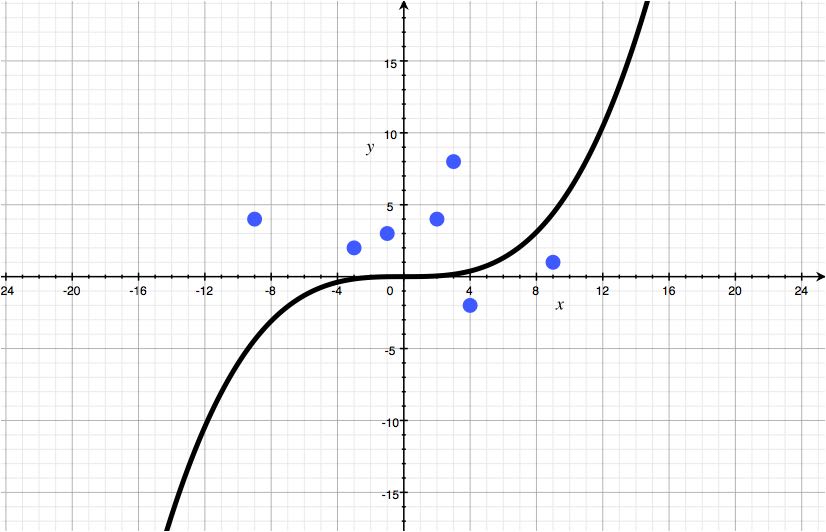
$M = 5$がなんか一番いい感じですね.