Chordal Graph: Minimal vertex separators

chocobaby-aporo.hatenablog.com

Chordal Graph回の第一回目です．今回はMinimal vertex separatorsを紹介します．

Minimal vertex separators

まず，$G = (V, E)$中の頂点集合$S \subseteq V$が，vertex separator (separator)とは 次のような2頂点$u, v$が存在することを言います．

• $u, v$は$G$中の連結成分に含まれるが，$G \setminus S$では同じ連結成分に含まれない．

この時，$S$は$u, v$をseparateすると言います． 簡単にいうと下の図のような頂点集合です．一応この例のグラフはchordalになっているはずです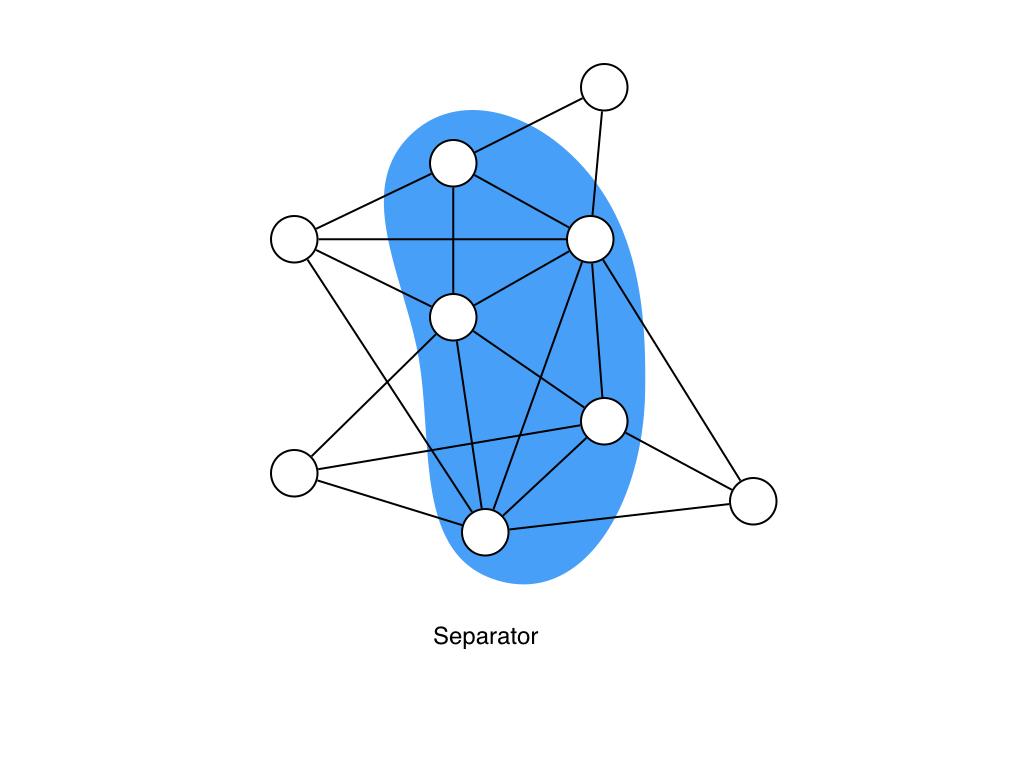． 特に，Minimal separatorというとSeparatorの中でもどんな頂点を除いてもseparator出なくなるようなseparatorです．

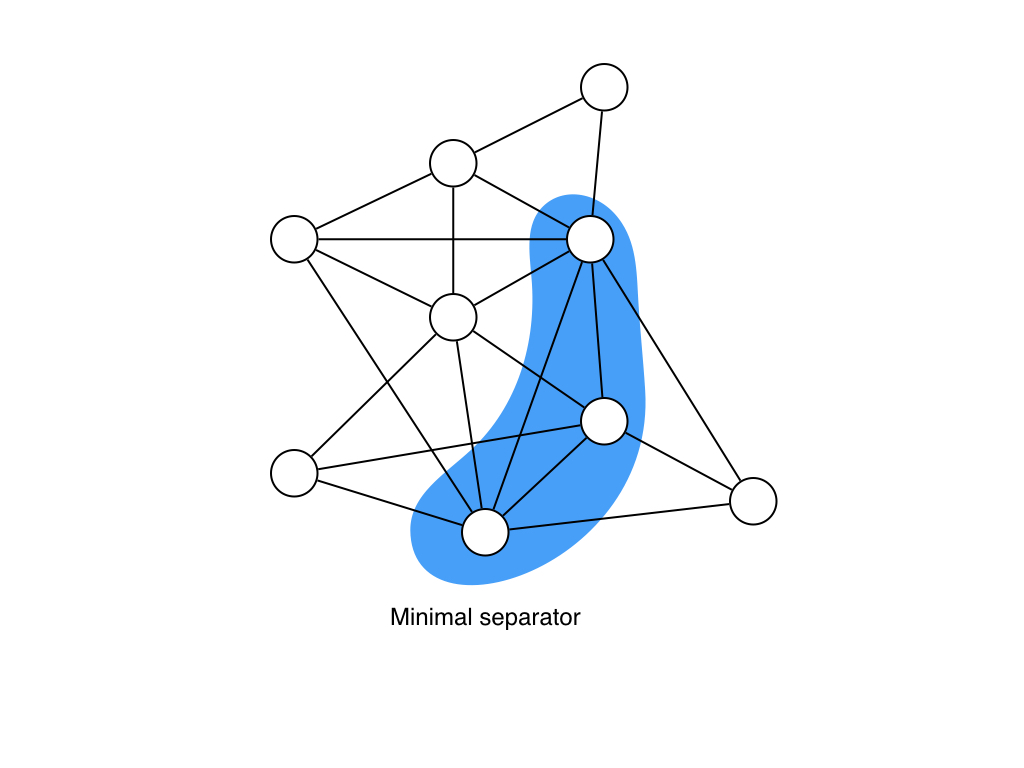
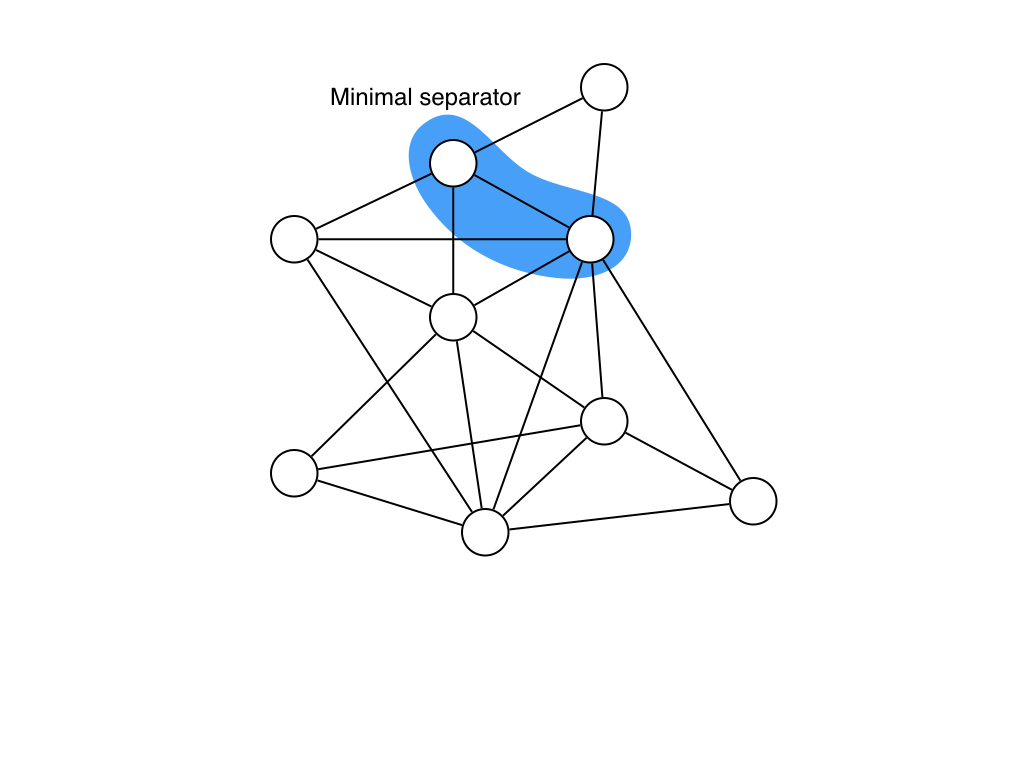
ここでChordal Graphの面白い性質1つ目ですが，次のような定理が知られています．

グラフ$G$がchordalである． $\iff$ $G$中の全てのminmal separatorがcliqueである．

$G$がchordalであるという条件を$A$，$G$中の全てのminmal separatorがcliqueであるという条件を$B$とします． まず$\lnot A \to \lnot B$，つまり$B \to A$について証明します． $G$がchordalではないので誘導部分サイクル（誘導部分グラフかつサイクル，要は弦を含まないサイクル）$C = (u_1, \dots, u_k)$が存在します．$(k \ge 4)$． この$C$中の隣接しない2頂点$u, v$をseparateするMinimal separatorを$S$とすると，この$S$は$C$中の隣接しない2頂点を含むのでcliqueではありません． したがって$B \to A$が成り立ちます．

次に$A \to B$を証明します． $S$を任意のminimal separatorとして，$G \setminus S$の連結成分の集合を$\sig C$とします． ここで重要なこととして，minimal separator $S$中の任意の頂点$u$は必ず$\sig C$中のすべての連結成分と隣接しています． もし全ての隣接成分と隣接していない頂点があると，minimal性が成り立たないからです．図で見るとこんな感じの状態になっています．

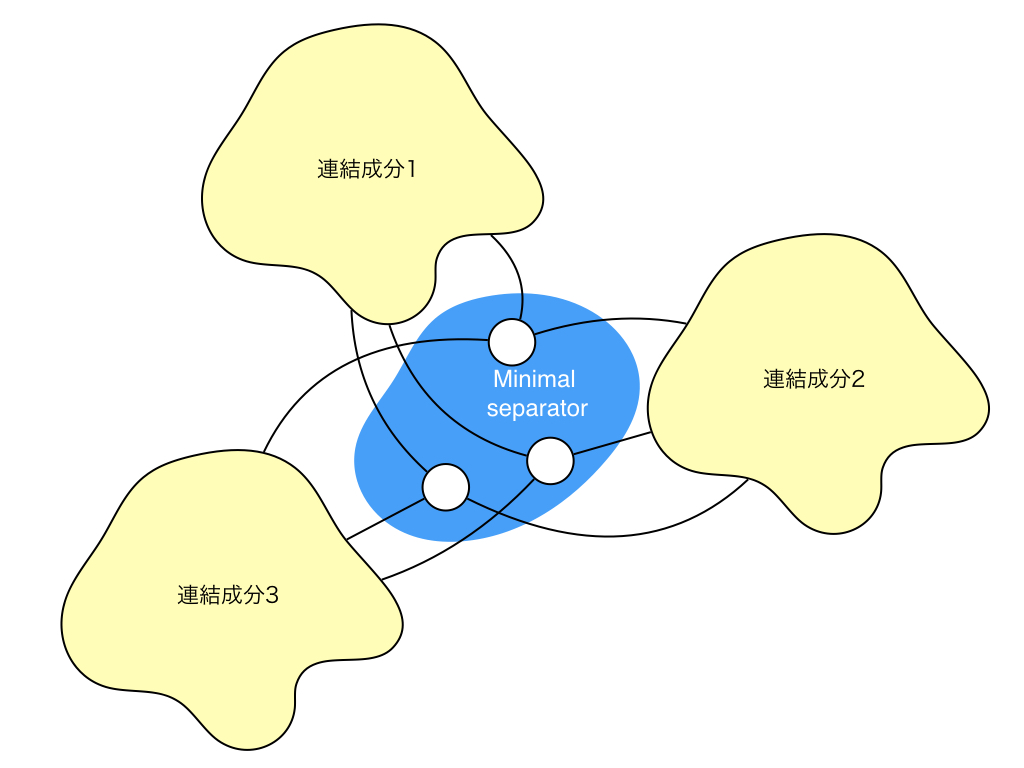
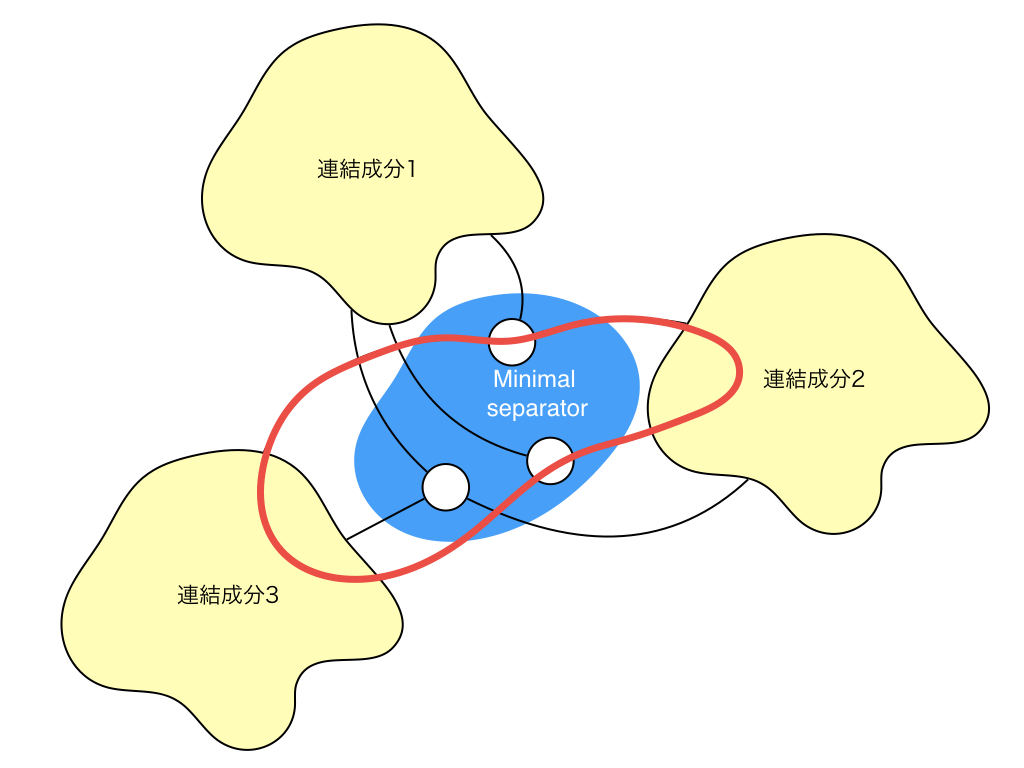
ここで，この性質から$S$中の任意の2頂点$u, v$は$G$中のあるサイクルに含まれることがわかります． しかも，そのサイクルの中には$S \setminus \set{u, v}$中の頂点を含まないサイクルも存在します． （要は$S$中の要素の$u$と$v$だけを含むサイクル）図中の赤線がそのサイクルを表しています． このサイクルは必ず長さが4以上なので，このサイクル中には必ず弦があります． この弦が$u, v$を結ぶ弦なら$u, v$は隣接するし，もし$u, v$を結ばないならその弦を含む$C$より短いサイクルができるため， 最終的には$u, v$を含む長さ4のサイクル$C'$ができます．ここで，$G$がchordalなので， $C'$も弦を含むのですが，$u$と$v$以外のサイクル中の頂点，つまり異なる連結成分同士の頂点を結ぶと，$S$がseparatorであることに矛盾するので， $u$と$v$を結ぶしかありません．つまり$S$中の任意の2頂点$u, v$は隣接しています．言い換えると$S$が誘導する$G $の誘導部分グラフ$G[S]$はcliqueになります．

まとめ

というわけで，Chordal Graphの面白い性質その1は

• グラフ$G$がchordalである． $\iff$ $G$中の全てのminmal separatorがcliqueである．

という性質でした．正直Choralの定義だけみて，「それなら全てのminimal separatorはcliqueになるのか〜」と気付く人はほとんどいないと思いますが， こんな面白い性質があることが知られています． まだまだ面白い性質があるので，気合が続く限り紹介していきます．

追記

今はまだ事実だけを書いておきますが，実はMinimal separatorの数はchordal graphの頂点数よりも少なくなることが知られています． それについての論文が出ていて，これですね． chordal graph以外でもminimal separatorの数については研究されています． あまり僕が理解していないので申し訳ないですが，一般のグラフでのMinimal separatorの数は O(1.6181ⁿ) なので， chordal graphではminimal separatorの数がすごく少なくなるのが知られています． 一般のグラフでのMinimal separatorの数の上限についてはここを参照してください．