近似アルゴリズムのお話し: Baker's technique

今年もデータ構造とアルゴリズムアドベントカレンダーの季節になってきました．これはカレンダー12日目の記事ですね．個人的な話ですが，去年度にようやく長い長い学生生活を終えたので，今年は隣の分野くらいのことをちゃんと勉強してみたいなぁと思い，いろいろ漁って勉強しました．TLの皆さんにはいろんな有用情報をいただいてありがとうございました！「このツイートしたら誰かいい情報教えてくれないかなぁ」と期待してツイートしたことが何度もありました．

そんなこんなで興味あったけどちゃんと勉強していなかったマトロイド，近似アルゴリズム，乱択アルゴリズムあたりをちゃんと本買って読んでみるか〜と思い，最初の1章とそれ以外を1つくらいは読んで，完全に理解しました．その中で，近似アルゴリズムが一番わかった感が強いので，自分の復習も兼ねて，近似アルゴリズムでよく使われるテクニックを1つ紹介しようかと思います．ちなみに僕は近似アルゴリズムを[1]で勉強して，今回は[2]の論文のテクニックを紹介します．

今回紹介するテクニックは1994年に発明されたBaker's techniqueとよばれるアルゴリズム構築技法です．これは入力が平面グラフのときに，最大独立点集合問題や，最小頂点被覆問題，最小支配集合問題といったNP-完全な問題に対し，PTAS（polynomial time approximation schem）を与えるアルゴリズム構築技法です．今の一文で未定義用語が5つくらい出ましたね．問題の名前はいいとしても，平面グラフと，NP-完全，PTASあたりは説明が必要かと思います．なので，次にそれらの用語の説明を簡単にします．

用語と今回の目標の説明

今回出てくる用語について簡単に定義します．正確でない定義も多々ありますので，正確な定義が知りたい方は申し訳ないですが，参考文献の方を見てください．

• 平面グラフ: 平面に辺の交差がなく描けるグラフのことです．グリッドなんかは平面グラフですね！正確には平面的グラフという気がしますが，今回は平面グラフと読んでしまいます．これはplanar graphとplane graphは実はちょっと違うという話と関係あると思っています．
• NP-完全問題: これは正確な定義がかなりややこしいので，ここではかなり多くの嘘を含みますが，多項式時間で解けないと信じられている問題の集合くらいに思ってくれれば大丈夫だと思います（プロの方が見ていたら生暖かい目で見逃してください）．
• PTAS: これは近似アルゴリズム分野の用語で，次のような条件を満たすアルゴリズムをPTASとよびます．最大化問題$\Pi$に対し，入力$I$とエラーパラメータ$\epsilon$（$\epsilon$は定数とみなす）が与えられたとき，最適解の値を$OPT$とすると，$(1 - \epsilon)OPT$を多項式時間で計算するアルゴリズム．

最小化問題に対するPTASは$(1-\epsilon)$が$(1 + \epsilon)$になります．計算時間の具体例としては，$O(|I|^{1/\epsilon})$時間と言った計算時間です．この時間で動作するアルゴリズムは$\epsilon$が定数なので，多項式時間で動作するとみなします．このとき，特に$|I|$と$1/\epsilon$の両方に関して多項式時間で動作するアルゴリズムはFPTAS（fully polynomial time approximation scheme）とよばれます．ナップサック問題なんかはFPTASを持つ問題の典型ですね．なので，この話を最大独立点集合問題を例に当てはめると，入力$I$が平面グラフ$G$で，エラーパラメータ$\epsilon$が与えられたときに，PTASを達成するアルゴリズムを与えます *1 *2

ちょっとした注意

この記事で紹介する方法では何度か木幅というグラフのパラメータを計算する必要があります．しかし，僕は実は木幅の厳密計算を理解していないので，今回の記事に書いてある方法だけでは近似アルゴリズムを作れません．しかし，入力グラフの木幅の値 $tw$ が$\epsilon$ を定数としたときに，定数であることが示せることと，定数 $k$ に対して，幅が $k$ 以下の木分解を計算する or 幅が $k$ 以上だと返すのは「線形時間」[6] *3でできるので，木幅は線形時間で計算可能だと思って記事を書いています．本音を言うとちゃんと元論文を読めばグラフの性質を使って線形時間で木幅がもっと簡単に厳密計算できそうに見えるのですが，まだそこまで理解していないです．ごめんなさい*4．

Baker's techniqueの概要

Baker's techniqueは現代の知識，特に木幅DPの知識を持ってみると実はすごい簡単なテクニックです．木幅に関するDPはきっと15日のゆらふなさんが書いてくれると思うので，今回はDPの詳細は省略しますが，木幅の定義は与えます．

大雑把にいうとBaker's techniqueは次のようなアルゴリズム構成法です．平面グラフ$G$の任意の頂点$v$を始点とし，$v$からの距離によって頂点を $V_0 = \{ v \}, V_1 , \ldots, V_{ n-1 } $ に頂点を分割します．この分割において，整数$j < k$に対し，$\bigcup_{ 0 \le i \le n/k } V_{ ik + j }$を削除します．直感的に言うと，距離 $k$ ごとにその距離を持つ頂点を全部消すと言う操作です．すると，グラフがいくつかの連結成分に分解されるのですが，実はこれらの連結成分は$k$-outerplanar graphと言い，$k$ が定数ならば，多くの難しい問題が簡単に解けがちなグラフになります．実際，$k$-outerplanar graph上では最大独立点集合は線形時間で計算できます．なので，このそれぞれの$k$-outerplanar graph上で，最大独立点集合を計算し，その和集合である独立点集合は実は良い近似比を達成すると言うテクニックです．そして，この $k$ の値を$1/\epsilon$ に設定すると近似比が $(1-\epsilon)OPT$ になり，計算時間も$n$ と定数$1/\epsilon$ に対して多項式時間になるので，PTASを達成します．

$k$-outerplanar graph 上での最大独立点集合問題

次に $k$-outerplanar graph の定義と，なぜ $k$-outerplanar graph上なら最大独立点集合が線形時間で解けるかを説明します．まずは定義からです．$k = 1$の時，つまり $1$-outerplanar graphはouterplanar graphともよばれ，平面描画するときに，全ての頂点が外面と接する様に平面描画できる平面グラフです．さらに，$k$-outerplanar graphとは平面描画したときに，外面と接する頂点を削除するという操作をすると $k - 1$ -outerplanar graphになるグラフです．$k$-outerplanar graphの具体例は次のようなグラフです．

このグラフだと外面に接する頂点削除を2回繰り返すとグラフが空にできるので，$2$-outerplanar graphです．

次に，平面グラフと $k$-outerplanar graph の関係を考えます． まず，平面グラフ中の頂点 $v$ に対し，先程の距離ごとに頂点集合を分割するルールを適用すると次のようになります．以下の例では 中心の頂点 $v$ を 頂点1にしています．

今回は$k=2$，つまり，$v$ からの距離が偶数の頂点を消した時の例を描いてみましたが，$k$を一般の場合にしてもだいたいこのように，中心から同心円状に頂点がのび，階層が$k$回に1回削除されるという構造になります．これをみると，削除されなかった頂点からなるグラフは，平面グラフの平面描画を考えると，外面に接する頂点削除を$k$回行うと空にできるので，これは$k$-outerpalar graphになります．

次に，$k$-outerplanar graphの木幅について考えます．木幅のお話は結構有名なので，他のブログにもありますね．

mizuwater0.hatenablog.com

それと日本語wikiもあります．

ja.wikipedia.org

あと，電気通信大学の授業もおすすめです．

http://dopal.cs.uec.ac.jp/okamotoy/lect/2016/treewidth/handout06.pdf

せっかくなので，電通大の授業スライドから定義を借りてくると，木分解の定義は次のようになります．

グラフ $G = (V, E)$ に対して，次の木 $\mathcal T$ を$G$ の木分解という

• $\mathcal T$ のノードは$V$の部分集合
• 各辺 $\set{u, v} \in E$に対し， $\set{u, v} \subseteq X$となるノード$X$が存在する．
• 各頂点 $v \in V$ に対し， $\mathcal T$ で $v$を含むノード$X$からなる誘導部分グラフは木になる．

具体例はwikiとか授業スライドを見るとわかりやすいと思います． ここで，ノード$X$の頂点数の最大値を$\mathcal T$の幅といいます．この条件を満たす分解はたくさんある（自明な木分解は$\mathcal T$が1ノードからなる木で，そのノードが全ての頂点を含む時）のですが，幅が最小である木分解の幅を$G$の木幅といいます． そして，実は$k$-outerplanarの木幅は $3k-1$ 以下であることが知られています[3]．

木幅が小さいグラフというのはめちゃくちゃ嬉しい性質が知られています．それはCourcelleの定理と呼ばれているのですが，次のような激ツヨ定理が知られています．

• 入力グラフ $G$ 木幅が定数であり，MSO（monadic second order logic）式 $\phi(X)$ が与えられた時，$\phi(X)$ を満たす要素数最大の $X$ は線形時間で発見できる．*5

MSOについてはここを参考にするといい感じです*6． 独立点集合は次のMSO式で書くことができます．

$\phi(X) = \forall u \in X( \forall v \in X( \set{u, v} \not\in E)$

この「MSOで記述できれば線形時間で解ける」という結果は激ムズなんですが，個々にアルゴリズムを作るのはそんなに難しくないことが多いです． きっとゆらふなさんの記事を読めば解けるようになると信じています． 大雑把には木分解の木があるので，その木の葉っぱからDPをするのですが，1ノードごとに状態数が$2^{k}$状態あるのでそれを全部覚えながらDPする感じです．なので，詳細は省きますが，独立点集合なら（確か） $O(2^{k} k^{2} n)$ 時間で解けます*7．今木幅は$3k-1$以下なので，$k = 1/\epsilon$に設定すると，この計算時間は $O(8^{1/\epsilon} (1/\epsilon)^{2} n)$ 時間になりますね．これをそれぞれの連結成分ごとに計算するので，総和は同じ計算時間で抑えられます．最後に，どの距離の頂点集合を削除するかが $k$ 通りあるので，$k = 1/\epsilon$回繰り返すため，全体の計算時間は $O(8^{1/\epsilon} (1/\epsilon)^{3} n)$ になります（注意: 木分解を計算する時間は考慮に入れていないです．）．これで計算時間はPTASの定義を満たしていますね！

あとは今計算した独立点集合の和集合がちゃんとサイズ$(1 - \epsilon)OPT$ 以上を達成するかどうかという近似比についての議論します．

アルゴリズムの近似比の解析

まずアルゴリズムの近似比の解析のために$S$を$G$中の最大独立点集合とします．今，グラフの分割をいくつか試しているので，分割の中で最も$| S \cap \bigcup_{0 \le i \le n/k}V_{ik + j}|$が小さい$j$ではサイズが$|S|/k$以下になります．実際にどの$j$がサイズを最小にするかはわからないのですが，これは全通り試しても$k$通りしかないため，これは全通り試し，サイズが最大な独立点集合を出力すればサイズを最大にする $j$ は見つけられます． したがって，得られる独立点集合のサイズは$(1 - 1/k) OPT$となります．よって，$k = 1/\epsilon$とすれば，近似比は$(1 - \epsilon)$を達成します．

Baker's techinqueの発展

平面グラフに対する効率良いアルゴリズムはかなり昔から研究されていて，グラフアルゴリズムの中心的な分野と言っても良いと思います．正直怖いのであまり手を出したくなかったのですが，これは意外と簡単だったので，ちょっと興味が出てきました．Baker's techniqueも90年代のテクニックだし， 平面グラフ上のアルゴリズムというメジャーなトピックなので，いろいろ発展系が研究されている様です．この辺りは本当によく知らないのですが，グラフの平面さを表すcrossing number（平面描画した時の辺の最小交差数）あたりでは研究がある様です[4]．それと風の噂によると，Bidimensionalityというのも発展系っぽいというのを聞きました[5]．なんか$k \times k$のグリッドグラフをマイナーとして含まないようなグラフに対するDPっぽいです．（あんまりわかっていない．）

なんかBaker's techniqueは結構簡単なテクニックかとおもっていたのですが，こうやって書いてみるとそれなりにいろんな知識が必要ですね．

参考文献

[1] Vazirani, Vijay V. Approximation algorithms. Springer Science & Business Media, 2013.
[2] Baker, Brenda S. "Approximation algorithms for NP-complete problems on planar graphs." Journal of the ACM (JACM) 41.1 (1994): 153-180. [3] Bodlaender, Hans L. "A partial k-arboretum of graphs with bounded treewidth." Theoretical computer science 209.1-2 (1998): 1-45.
[4] Grigoriev, Alexander, and Hans L. Bodlaender. "Algorithms for graphs embeddable with few crossings per edge." Algorithmica 49.1 (2007): 1-11.
[5] Cygan, Marek, et al. Parameterized algorithms. Vol. 4. No. 8. Cham: Springer, 2015.
[6] Bodlaender, Hans L. "A linear-time algorithm for finding tree-decompositions of small treewidth." SIAM Journal on computing 25.6 (1996): 1305-1317.

*1:元論文は $O(8^{1/\epsilon} (n + m) )$ で，僕の今回のアルゴリズムは $O(2^{2^{1/\epsilon}} (1/\epsilon)^{3} n)$ くらいなので，めっちゃ負けていますが，PTASにはなります．

*2:木幅計算パートを無視すると，$O(8^{1/\epsilon} (1/\epsilon)^{3} n)$ になります．

*3:定数項がえげつないです．ざっと見積もっても $2^{2^{k}}$ は軽くあります

*4:PTASを与えると言う結果には矛盾しないので許してください！

*5:記述が間違っていたらごめんなさい

*6:この授業スライドは他のトピックも非常に面白いので，おすすめです．僕はマトロイドも結構ここのスライドで勉強しました．

*7:$k^{2}$ の部分が自信ないですが，$poly(k)$ なのは間違い無いです．

オレンジグラフの別解（TLEしました．）

昔昔にオレンジグラフという問題が出ていましたね． atcoder.jp

これはどういう問題かというと，グラフが与えられるので，極大な部分二部グラフ（これ以上二部性を保証しながら辺追加ができない部分二部グラフ）の列挙が想定解法なのですが，計算時間が $O(m 2^n)$ 時間と指数的に時間がかかります．

列挙アルゴリズムではこのように指数時間かかるのはそもそも答えの数が指数個あるので，ある種しょうがないのですが，この答えの個数というバウンドを使ってしまうと面白みがなくなる問題もいろいろあります．例えば，線分の集合が与えられた時に，その交点を列挙しろという問題では，$n$を線分の個数とすると，ナイーブアルゴリズムは $O(n^2)$ 時間で動作します．しかも，最悪時，交点の個数は $O(n^2)$ なので，このナイーブアルゴリズムが最適になってしまいます．なんかこれでは面白くないということで，答えの個数を$M^{}$とおき，$M^{}$と$n$を使って計算量を見積もるというアルゴリズムが開発されてきました．交点列挙なら，確か $O( ( n+M ) \log n)$で列挙できたと思います（自信ない）．このように解の個数と入力サイズの2つを用いて計算量が抑えられるアルゴリズムを出力依存型アルゴリズム（Output sensitive algorithm）と言います．

ここで自然な疑問として，今回のオレンジグラフもOutput sensitiveに解けないのか？という疑問があります．実はこれは解くことができます！具体的には今回実装したアルゴリズムは $O(M m^2)$ 時間，$O(M m)$領域のアルゴリズムになっています．ちなみに本当のことを言うと実装をサボるために時間が$O(M m^2 \alpha(2n, n) )$ 時間になっています． $\alpha(2n, n)$ はいつも通りunion findの計算量です．noshi91さん，実装のアドバイスありがとうございました！．

noshi91.hatenablog.com

正当性の証明は結構めんどくさいのですが，アルゴリズムはめっちゃ簡単です．正当性に関する解説はここですね．

qiita.com

ざっくり証明のアイディアを説明すると，こんな感じです．基本的に，極大部分二部グラフ（MB）から別のMBを作るのはそんなに難しくなく，たくさん答えを見つけることはできます．具体的にはあるMBを1つ見つけてから，そのMBに含まれない辺1つからなる部分グラフは二部グラフなので，それに適当に辺を追加し，MBを作れば別なMBを作ることができます．なので，問題は全てのMBを出力できているかです．これを証明するためには，MBとMBの間に距離のような指標を定義してあげるというアイディアが結構うまくいきます．これは何をしたいかというと，MBを1つの頂点だと思い，MBから別のMBを作るルールを有向辺だと思った時にできるグラフを強連結にしたいという思想から来ています．もしこのルールで作られたグラフが強連結なら，適当にBFSやDFSすればMBが列挙できますね．ここで，強連結の定義を思い出すと，「任意の頂点ペア $u$ と $v$ について $u$-$v$ パスが存在する」でしたね．このパスの存在性を示すために， $u$ から $v$ に到達可能であることを示す必要があります．そのため， 今のMBから別のMB'に到達可能ということを示すため，MBとMB'の間にある指標を定義し，その指標を小さく or 大きくするMBに到達できるということを示すというのが一つの戦略になります．いろいろ言いましたが，最後に結論だけ言ってしまうと，MBの頂点ID最小の頂点からBFS順に辺を並べて，その辺の列のprefixをどんどん伸ばしていくということをやっていけば必ず欲しい解MB'に到達できるよ〜というお話しです．以上が証明の気分でした．

具体的なアルゴリズムは以下のとおりです．

• 適当にMBを求める．
• 得られたMBをキューに突っ込み，キューが空になるまで以下を繰り返す．
  • キューからMBを一つ取り出す．
  • MBに含まれない辺$e = \set{x, y}$を選択し，MBから$x$に接続した辺を全て削除して得られるMBxと$y$に接続する辺を全て削除して得られるMByを作る．
  • MBxとMByに適当に辺を追加して極大な二部グラフを作る．得られた極大二部グラフがまだ出力していない解ならば，キューに突っ込む．

というわけで意気揚々とAtCoderさんに投げたのですが，TLEしました！（悲しいね）．僕が思ったより答えの数が多かったようで，多項式倍の部分で勝てなかったようです．．． 結構このアルゴリズムの実装は楽チンで，union find partとデータの受け取りとか除くと大体50行くらいでかける感じでした．

以下ソースコードです．

#include<iostream>
#include<queue>
#include<set>
class edge{
public:
    int x, y;
};
class UnionFind{
public:
  UnionFind();
  UnionFind(int _n){init(_n);}
  void init(int _n){
    n = _n;
    if(rank.size() == 0)rank.resize(n), parent.resize(n);
      for (int i = 0; i < n; i++) {
      rank[i] = 0;
      parent[i] = i;
    }
  }
  int find(int x){
    if(x == parent[x])return x;
    else return parent[x] = find(parent[x]);
  }
  
  void unite(int x, int y){
    x = find(x);
    y = find(y);
    if(x == y)return;
    if(rank[x] < rank[y]){
      parent[x] = y;
    }else{
      parent[y] = x;
      if(rank[x] == rank[y])rank[x]++;
    }
  }
  bool same(int x, int y){
    return find(x) == find(y);
  }
  int size(){
    int res = 0;
    for (int i = 0; i < n; i++) {
      if(parent[i] == i)res++;
    }
    return res;
  }
private:
  int n;
  std::vector<int> rank, parent;
};

UnionFind uf(40);
 
std::vector<int> Maximize(std::vector<edge> &G, int n, std::vector<int> &subg){
    uf.init(2*n);
    for(int i = 0; i < (int)G.size(); i++) {
      int x = G[i].x, y = G[i].y;
      if(subg[i] == 1) uf.unite(x+n, y), uf.unite(x, y+n);
    }
    for(int i = 0; i < (int)G.size(); i++) {
      int x = G[i].x, y = G[i].y;
      if(subg[i] == 0){
          subg[i] = 1;
          if(not uf.same(x+n, y+n)) uf.unite(x+n, y), uf.unite(x, y+n);
          else subg[i] = 0;
      }
  }
  return subg;
}
 
void EnumerateNeighborhoods(std::vector<edge> &G, std::vector<int> &subg, int a, int n, std::set<std::vector<int> > &ans, std::queue<std::vector<int> > &que){
    std::vector<int> S = subg;
    for(int i = 0; i < (int)G.size(); i++) {
        if(G[i].x == G[a].x or G[i].y == G[a].x)S[i] = 0;
    }
    S[a] = 1;    
    Maximize(G, n, S);
    if(ans.find(S) == ans.end()){
        ans.insert(S);
        que.push(S);
    }
 
    S = subg;
    for(int i = 0; i < (int)G.size(); i++) {
        if(G[i].x == G[a].y or G[i].y == G[a].y)S[i] = 0;
    }
    S[a] = 1;
    Maximize(G, n, S);
    if(ans.find(S) == ans.end()){
        ans.insert(S);
        que.push(S);
    }
}
 
int main(){
    int n, m;
    std::cin >> n >> m;    
    std::vector<edge> G(m);
    std::set<std::vector<int> > ans;
    for(int i = 0; i < m; i++) {
        int from, to;
        std::cin >> from >> to;
        G[i].x = --from, G[i].y = --to;
    }
    std::vector<int> subg(m, 0);
    Maximize(G, n, subg);
    std::queue<std::vector<int> > que;
    que.push(subg);
    ans.insert(subg);
    while(not que.empty()){
        subg = que.front();
        que.pop();
        for(int i = 0; i < m; i++) if(subg[i] == 0) EnumerateNeighborhoods(G, subg, i, n, ans, que);
    }
    std::cout << ans.size() << std::endl;
}

辞書順幅優先探索Lex BFS（Chordal Graph 5回）

この記事はデータ構造とアルゴリズムアドベントカレンダー 2018の19日目の記事です．

qiita.com

とりあえず懺悔します．遅れて申し訳ありません．

データ構造とアルゴリズムアドベントカレンダーで列挙とかの話をしようかなぁとか思ったのですが，書くのが大変だったのと， これ読みそうな人類って誰だ？という気持ちになったので，ちょっと違う話をしようと思います． なので，今回は探索アルゴリズムの基本とも言える幅優先探索の亜種である辞書順幅優先探索について書いていきます． （ちなみにこの記事は1年くらい更新していなかったChordal Graphの第5回も兼ねています．） 今回のネタ本はこんな感じです． Graph Classes: A Survey Algorithmic Graph Theory and Perfect Graphs

グラフ探索アルゴリズム

有名なグラフ探索アルゴリズムとして幅優先探索（breadth first search, BFS）と深さ優先探索（depth first search）があります． これらは（多分）情報系の大学に行くと2年生か3年生くらいに習って，多分授業で実装をする機会もあるくらい有名なアルゴリズムだと思います． しかも，これらのアルゴリズムはグラフ探索だけでなく，メモリと時間を気にしさえしなければ（指数時間，指数メモリを許せば）いろんな問題がこの2つの探索で解くことができます． グラフ探索っぽくない幅優先探索の使い方でよくあるのは次のような問題ですかね？

• 15パズルを完成させる最短手数を求めよ

これらのグラフ探索アルゴリズムは簡単ですが，実は使い勝手が良く，いろんな問題がDFSやBFSっぽい考えで解くことができます．

• グラフ上の最短経路問題: BFS
• グラフ上の最短閉路問題: BFS
• グラフの平面性判定: DFS
• 関節点や橋の列挙: DFS
• 有向グラフの強連結成分分解: DFS

（何か他にいい例を知っている方がいたら教えてください．．．）

そんなBFS，DFSの中で，今回は少し変わったBFSであるLex BFS（Lexicographical BFS）を紹介しようと思います． これはほぼBFSと同じなんですが，キューに次の頂点を追加する際，少しだけ追加の順序が異なります． 通常のグラフ探索のBFSする場合，ある頂点$v$をみて，$v$の隣接頂点をキューに追加する順番は適当で良いのですが， Lex BFSではちょっと頭を使ってキュー中の順序を管理します．

Lex BFS

Lex BFSの疑似コードは次のようになります．まずは前提として，$G$中の任意の頂点$v$は1つの文字列$S_v$を持っていると思ってください． 初期値として$S_v = \emptyset$とします．また，以下では数字を文字のように扱います．文字列は数字の列だと思ってください．

$LexBFS(G)$ 入力: グラフ$G$，頂点数 $n$ ，辺数 $ m $

1. $G$の任意の頂点$v$は文字列$S_v = \emptyset$を持ちます．
2. $G$中の頂点で辞書順最大の文字列を持つ頂点$v$を選ぶ．（もし辞書順最大が複数ある時はその中から任意に選んで良い．）
3. $v$の隣接頂点$u$が持つ$S_u$の末尾に文字$n$を追加します．
4. $n$を1つ小さくして，2行目の処理に飛びます．

実行例はこんな感じです．

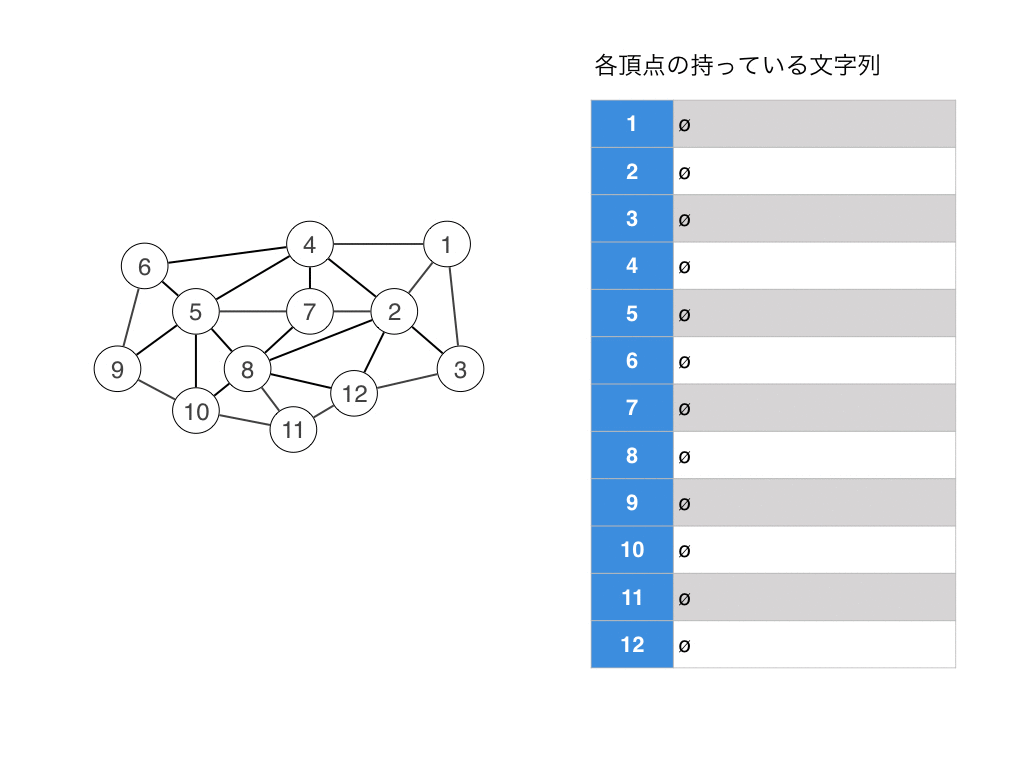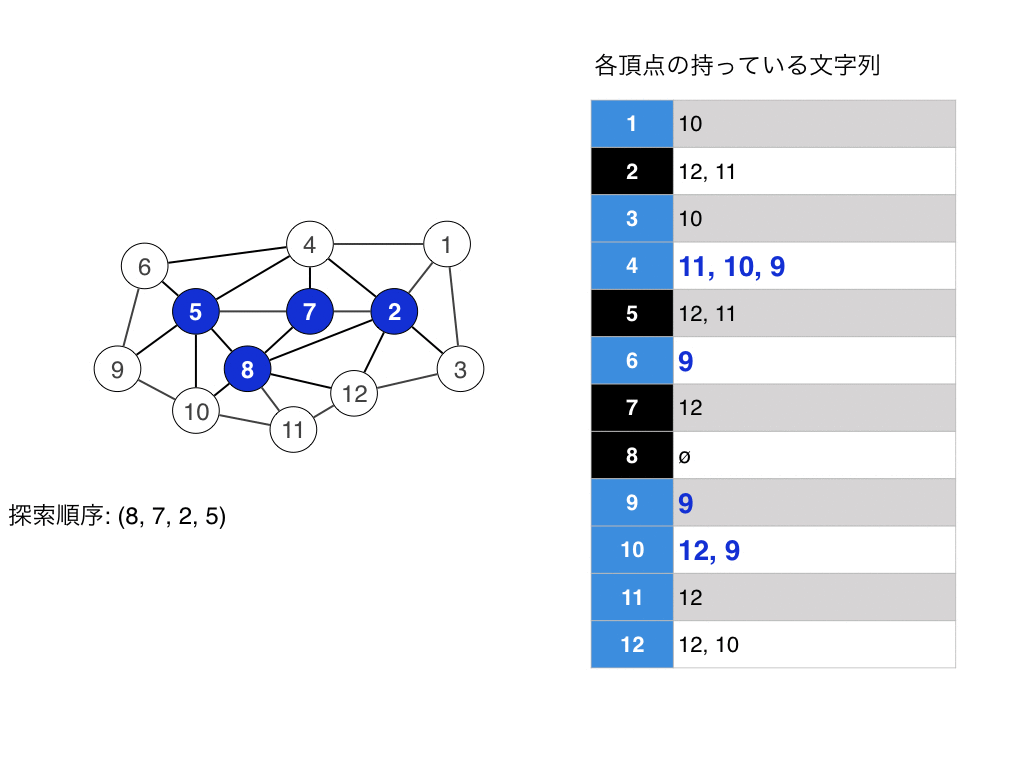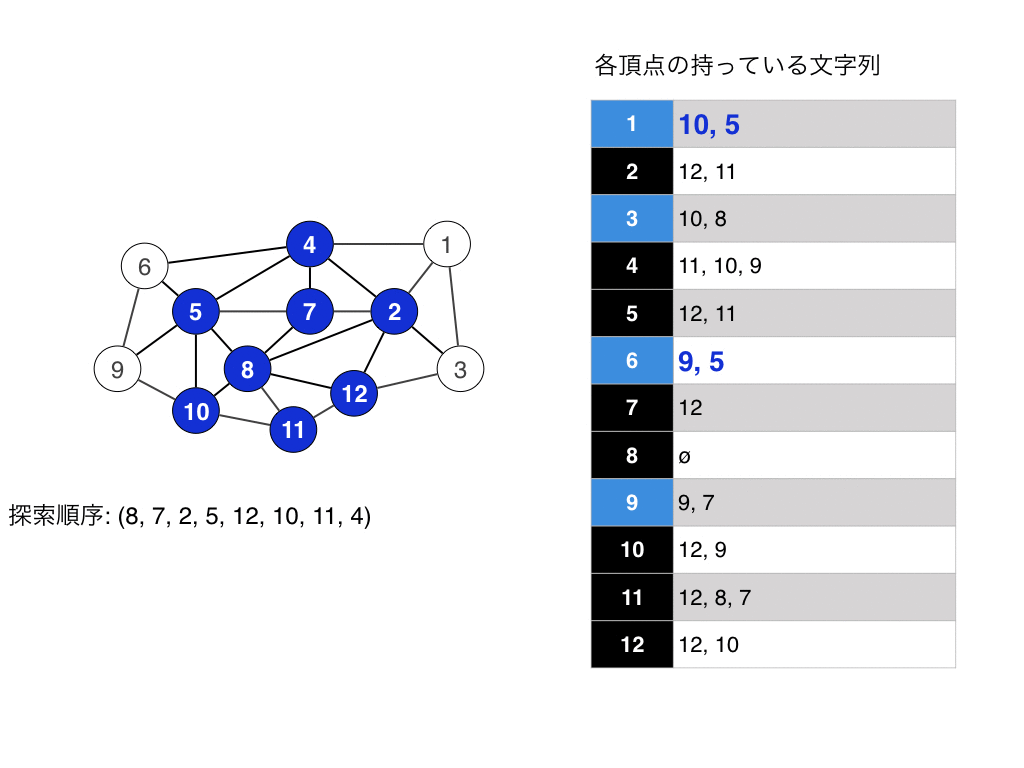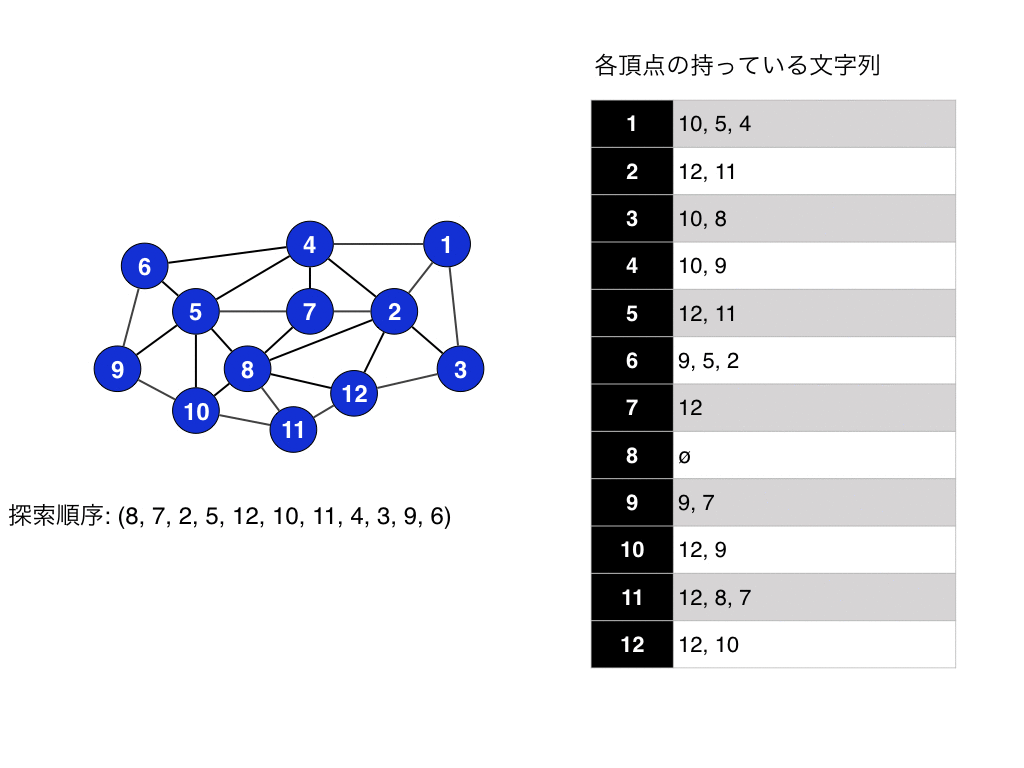
実はLexBFSはコーディングを頑張ると線形時間で実装できます． 実装をwikiを見るとなんとなくわかると思います． 簡単にいうとリストと$n$個の番兵的なものを使うと実装できると思います．

Lex BFSを用いたグラフのChordality判定

実はこのLexBFSを使ってグラフがchordal graphかどうかの判定問題が解けます． 方法は簡単で，Lex BFSをして求めた頂点の探索順の逆順がPerfect elimination ordering (PEO)かどうかを確かめるだけです． 実際に(8, 7, 2, 5, 12, 10, 11, 4, 3, 9, 6)の順序を逆にした(6, 9, 3, 4, 11, 10, 12, 5, 2, 7, 8) は入力グラフ$G$のPEOになっています． ここで，PEOの定義は次の通りです．頂点順序$σ = (v_1, v_2, ..., v_n)$が任意の$v_i$に対して，$v_i$から$v_n$を用いて作る誘導部分グラフ$G'$の中で$v_i$がsimplicial vertexであるとき，$σ$をPEOと言います．また，ある頂点$v$がsimplicial vertexであるとは，$v$とその隣接頂点からなる誘導部分グラフがクリークになることを言います．

では，この順序がきちんとPEOになっていることを証明してみます． と思ったのですが，本当に申し訳ありませんが，証明はもう少し後に公開します． （完全に理解していない + 時間が足りない）

　LexBFSの他の使い道

LexBFSは他にも使い道があって，次のグラフクラスの認識にも使えるようです．

• HHD-free graph
• distance-hereditary graph
• interval graph
• co graph graph

この辺りのこともいつか書いて見たいですね．

木の同型性判定のお話

この記事は文字列アドベントカレンダー5日目の記事です．

qiita.com

はじめに

文字列Advent Calendarと言いつつ，木について書いていこうかなと思います． まあ，文字列ガチ勢から見れば，根付き木は実質文字列なので，このCalendarで書いてもみんな喜んでくれると信じています． あと，実際ここで紹介する手法でも木を文字列に変換してから色々やって，木の同型性を判定します．

紹介内容

今回紹介するのはタイトル等にもあるように，木の同型性判定問題を線形時間で解くアルゴリズムの紹介をします． 木のお話をする前にグラフの同型性判定問題について説明します．グラフの同型性判定問題とは，2つのグラフ$G$と$H$が与えられた時，$G$と$H$の頂点間に辺の有る無し関係を変えないような頂点の対応付けがありますか？というYes/No問題に答える問題です． 木の同型性判定問題とは，この入力グラフ$G$を木に限定した場合にどうやったら解けるの？という問題です．

根付き木の同型性判定問題

いきなり木に限定するとよくわからないので，根付き木の同型性判定から紹介しましょう． 以下この節の説明では木といったら根付き木と思ってください． この内容はこのPDFと このスライドの内容です． また，スライド中のAHUアルゴリズムは[1]の本の内容です． 僕は本が手に入らなかったので，スライドで勉強しました，

ここでは文字列ガチ勢の人々が大好き（と思われる）テクニックである，木の文字列への変換を使います． 木の同型性判定のアルゴリズムの概要をざっくり説明すると，木をあるルールで文字列にして，

• 変換後の2つの文字列が同じである $\iff$ 2つの木が同型である

という変換ルールを与えるというアルゴリズムです． 木を括弧列に変換する方法は簡単で，次のように変換します．

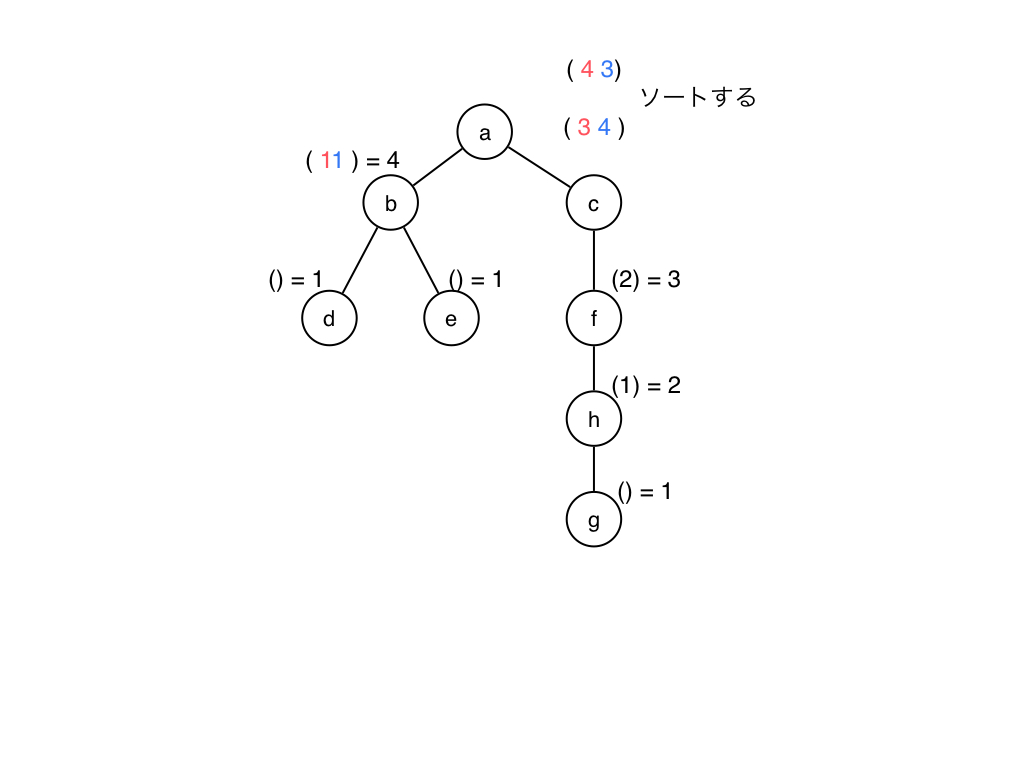
これは葉を"()"とし，中間ノードは子供を1列に並べて両端を"("と")"でまとめるといった操作で 木を文字列に変換します．中間ノードに対応する文字列を生成する場合，子供の文字列をソート順で 連結するようにします．結論から言うと， 実はこの文字列が一致していることと木が同型であることが同値な条件になっています． 以降はこの正当性についてて見ていきます． 正当性のきちんとした証明を見ようと上記のスライドと資料を見たら"明らかである．"，"証明は簡単だ"と書かれていました． 悲しい．．． ゆるふわに証明らしき物を考えてみます． まずは

*　括弧列が同じである $\to$ 木が同型である．

ですが，こちらは問題なく正しそうに見えます．次に

• 木が同型である　$\to$ 括弧列が同じである．

を考えてみます． これは正しそうで，帰納的に考えると， 高さ$0$の木は自明に同型ならば括弧列が同じになります． 高さ$k$以下の木は正しく括弧列が同じくなるとし， 高さ$k + 1$の木を考えます． この時，根を親に持つ頂点以下のそれぞれの部分木を考えて，それらの部分木を文字列に変換すると， それぞれの部分木は高さ$k$以下なので，木が同型ならば括弧列が同じになります． その括弧列をソートしたとすると，元の木の文字列も一意に定まり， 木が同型ならば括弧列が同じになります． こんな感じに帰納法的に考えるとこの条件が正しい気がして来ます．

次にこのアルゴリズム（以降ではAHUアルゴリズムと言います．これはAho，Hopcroft，Ullmanの頭文字から来ています．） の時間計算量を考えます．これは最悪ケース各ノード $O(n)$ 文字持つことになるので $O(n²)$ 時間アルゴリズムです． AHUアルゴリズムを線形時間になるように改良します．

と思いましたが，時間の関係上とりあえず割愛します．（気が向いたら更新しときます．） 雰囲気で説明すると下の図のように毎回文字列を整数値1つに書き換えます．

木の同型性判定

先ほど与えた根付き木の同型性判定問題を解くアルゴリズムを使って木の同型性判定を解きましょう． ここで，グラフには中心という頂点が存在します． 中心の説明の前にグラフの半径(radius)について定義します． ここで，$G$中の任意の頂点$u$とした時，$v, u$間の距離を$d(u, v)$と定義します． グラフ$G$中の$v$が$G$の中心であるとは，$max_{u \in V}(d(u, v))$が最小な頂点$v$を$G$の中心と言います． つまり，どんなに遠くに行こうとしても最短パスしか通れないならあんまり遠くに行けない頂点ということです．

そして木が同型なので，

• 木が同型である $\to$ $G$の中心は$H$の中心に対応付けられる

ということがわかります． したがって，同型ならば少なくとも中心は等しくなります． この性質より，根無し木を，木の中心同士を根と思って 根付き木にとし，根付き木の同型性判定アルゴリズムを使えば終わりです． また，木には中心が高々2つしか存在しないので，定数回の AHUアルゴリズムの適用で判定ができます． したがって根無し木も $O(n)$ 時間で同型性が判定可能です．

非常にゆるゆるで申し訳ないですが， こんな感じで木の同型性判定が行えます．

僕は$O(n \log n)$の雑実装でこんな感じで実装しました．

参考文献

1. Aho, Alfred V., and John E. Hopcroft. The design and analysis of computer algorithms. Pearson Education India, 1974.

Chordal Graph: Maximum Cardinality Search

今回はグラフの性質のお話ではなくPEOを求めるためのアルゴリズムのお話をします． MCSとLex BFSというアルゴリズムのお話をします． chordal graphの性質についてはこの2つのアルゴリズムを説明した後にもまだまだ書きます．

今回は長くなるので，2回に分けました． PEOを求めるアルゴリズムだけ知りたい人は今回のMCSの部分だけ読むとわかると思います． ただ，Lex BFSはMCSよりも便利な印象があって，Lex BFSを使うと他の問題も解けるようです． 例としてあげられるのは1つしか知りませんが，入力グラフ$G$がCo-graph($P_4$-free graph)，つまり， 誘導部分グラフとして長さ4のパスを含まないグラフかどうかの判定問題もLex BFSで解けるらしいです． 論文とかではなく，ネット上の資料ですが，こんなスライドがあって，紹介されています． 多分競プロerなら知っていると思いますが，hosさんのスライドです． こちらはブログでは紹介しなさそうな予感です．気が向いたらするかも？

今回のお話に入っていきます．前回PEOという順序があることとグラフがchordalであることが同値であることはわかりました． でもPEOを計算できないとグラフがchordalかどうかを確かめられないので悲しい気持ちになります． しかし，PEOはグラフサイズに対して線形時間で求めるMCSとLex BFSという2つのアルゴリズムがあります． 今回はそのうちの1つのMCSを紹介します．Lex BFSは次回説明するのでお楽しみに！

Maximum cardinality search

まずはアルゴリズムの動きを説明した後で，アルゴリズムの正当性を証明します． 計算時間の解析はほぼ自明なので，特にはしません． MCSは，単純にいうと貪欲に次数の大きい頂点から頂点をとっていくだけのアルゴリズムなのですが， どういったグラフの中で次数が大きいのかを考えるのがキモになります．当然ですが，入力グラフ$G$を 考えて，そこから次数の大きい順に頂点を選んで順序付してもPEOにはなりません．

そこで，入力グラフ$G = (V, E)$に対してどういったグラフを考えるかというと， 二部グラフっぽいグラフ？$H = (X, Y, E)$を考えます． ここで，$H$は，$X \cup Y = V$かつ$X \cap Y = \emptyset$を満たします．辺集合は$G$と$H$は同じです． $X$間の2頂点や$Y$間の2頂点にも辺はあるので，二部グラフではないのですが，それに近いイメージです． つまりは頂点集合を2つに分割したグラフを考えるということですね．図にするとこんな感じです．

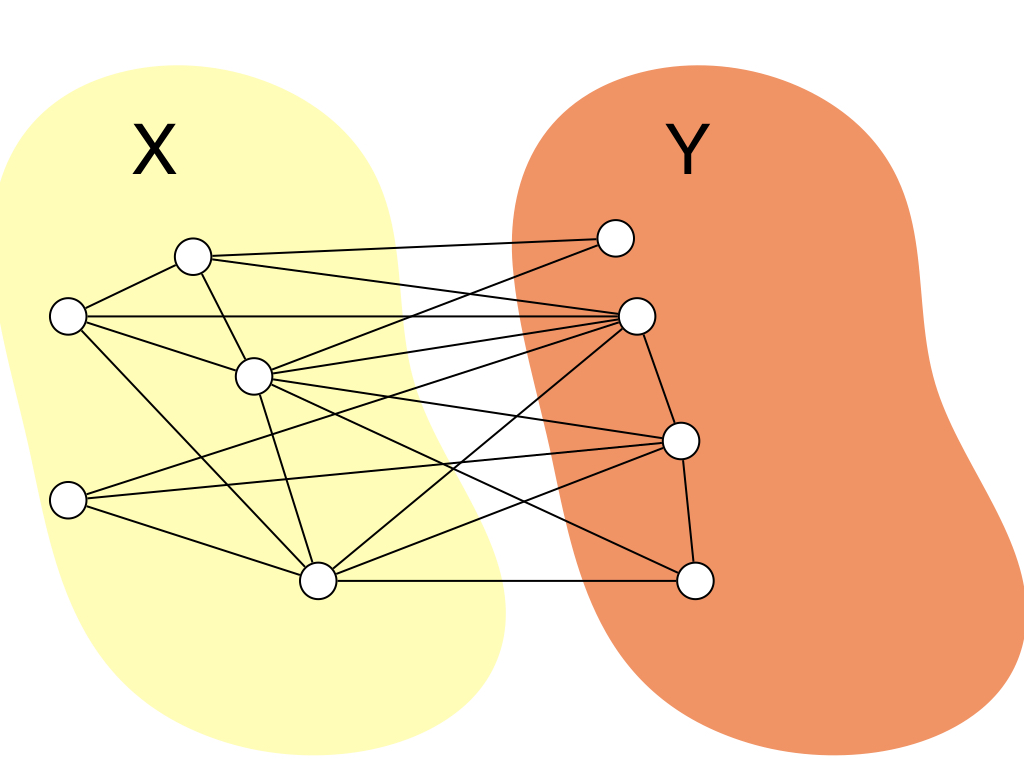
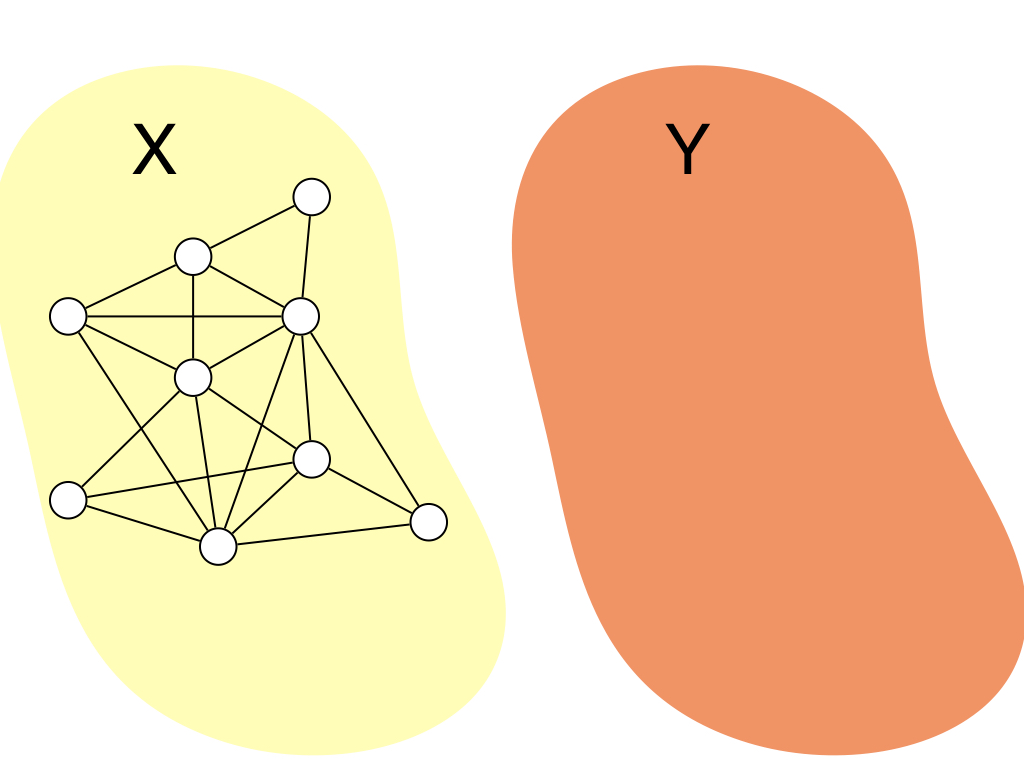
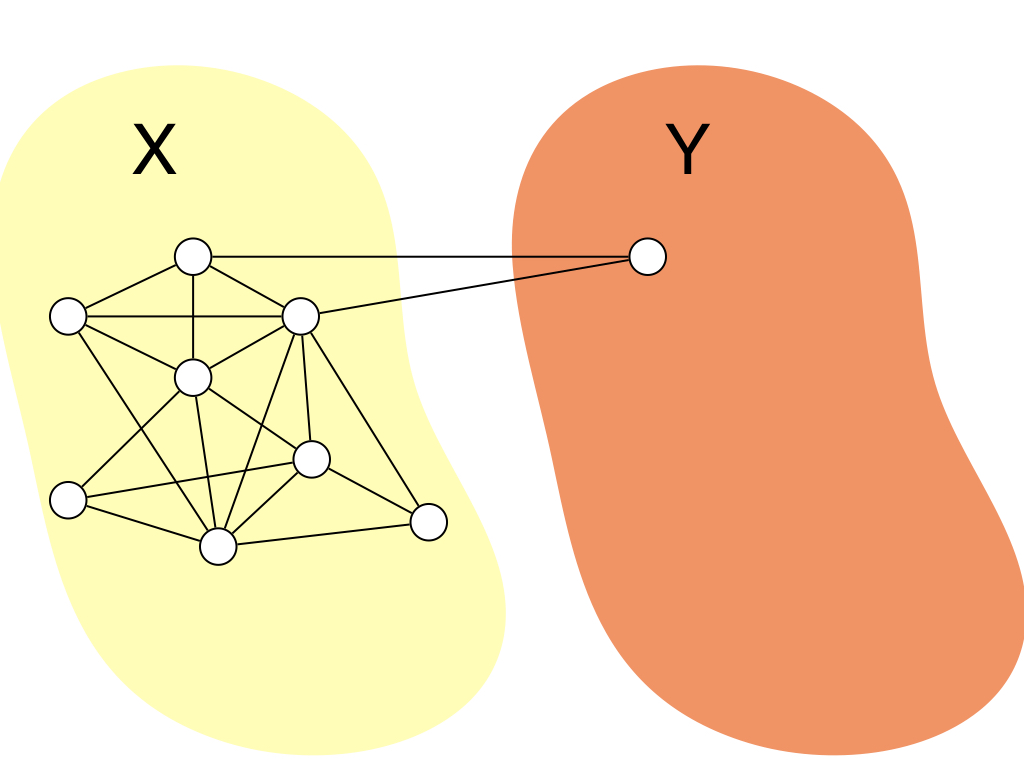
$H$は初期状態として，$X = V$，$Y = \emptyset$を満たすとします．ここで，$\size{N(v) \cap Y}$が最大になるような 頂点$v \in X$を選択します．また，$\size{N(v) \cap Y}$の値が同じ$v$が複数ある場合はそのうちの任意の1つを選択します． そして，$v$を$X$から$Y$に移動させます．つまり$H' = (X \setminus \set{v}, Y \cup \set{v}, E)$というグラフに更新します． これを$X$が空集合になるまで繰り返します． すると，グラフがchordalであれば必ずこの頂点の追加順の逆順がPEOになります． 証明は後で行います． ここでは，順序付の逆順をMCS順序と呼ぶことにします． ただし，この順序はchordal graphでなくても定義できるので，本当にMCS順序がPEOになっているかはチェックする必要はあります． ここで保証されるのは，$G$がchordalであればMCS順序が必ずPEOになるということ保証します． アルゴリズムの動きはこんな感じですね．

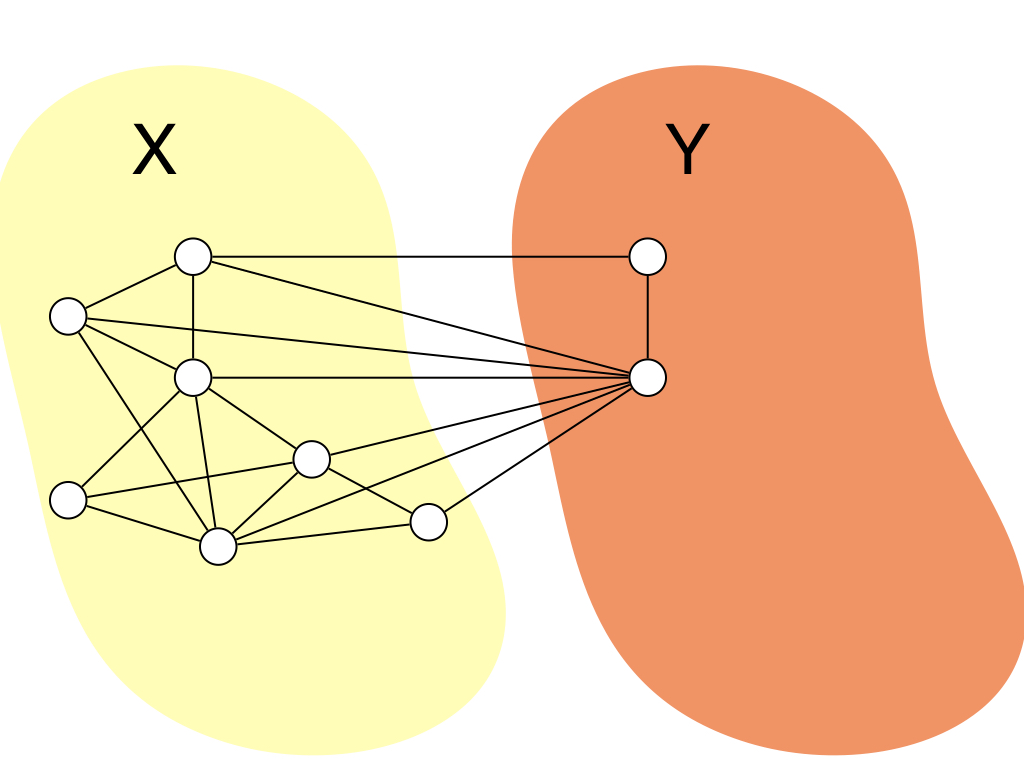
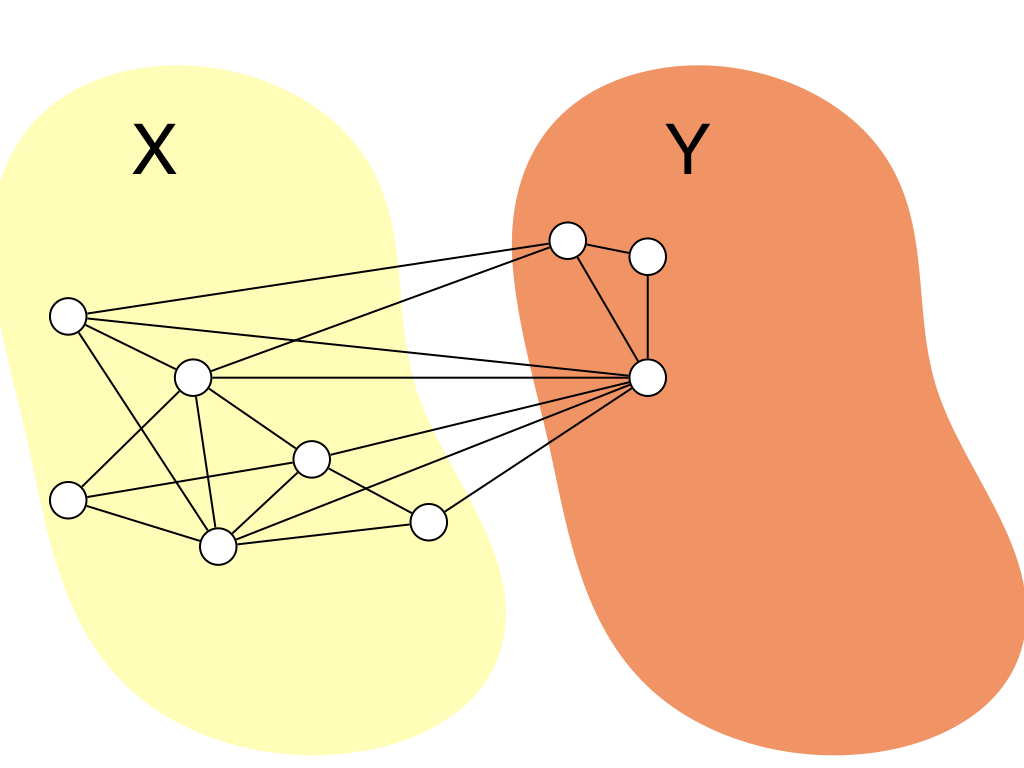
ついでに大雑把に計算時間についていうと，このアルゴリズムを線形時間で実装する方法は色々あると思うのですが， $X$中の頂点集合の次数順ソートした頂点列を持っていて，$X$から$Y$に頂点が移動するたびにそれを更新すれば $O(\Delta)$時間で1つの頂点を移動できるので，全体で$O(n + m)$時間で計算できます．（$n$と$m{}$ は頂点数と辺数） ソートには$O(n \log n)$かかるんじゃね？っと思うかもしれないですが，次数はたかだか$n$しかないので， バケットソートすると線形時間でソートできます．色々自分のやりやすい実装を考えてみてください． （記事を見ている人は競プロerが多い想定なので，いい実装を思いついてくれそう）

MCSの正当性の証明

これ以降は正当性の証明です．ここでは，MCSで作る任意の順序付を$\alpha$とします． これ以降では頂点番号はの順序で番号を振り直したと考えてください． 例えば，頂点数4のグラフがあって，$\alpha = (3, 2, 4, 1)$だったら， 3を1に，2を2に，4を4に，1を4に番号をつけ直したと考えてください． グラフがchordalである場合，この順序が必ずPEOを出力することを証明します． 今回は直接これを証明する前に次の補題を証明します． ここで，$V_i$は頂点番号$i$から$n$までの頂点を含む集合とし， 頂点$v$の頂点番号を$id(v)$と表記することにします．

$\alpha$がPEOではない $\iff$ ある頂点$v_i$に対して，$v_i$から$v_j \in V_{i + 1}$までの$ V \setminus V_{i+1} $を通る長さ2以上のchordless pathが存在する．

chordless pathとはpath $P = (v_1, \dots, v_k)$の任意の頂点$v_i$が$v_{i - 1}$と$v_{i + 1}$以外の頂点と隣接しないpathです． ちょっとこの補題が何を言っているのかわかりにくいと思うので，この補題が表す状態を図にするとこんな感じです．

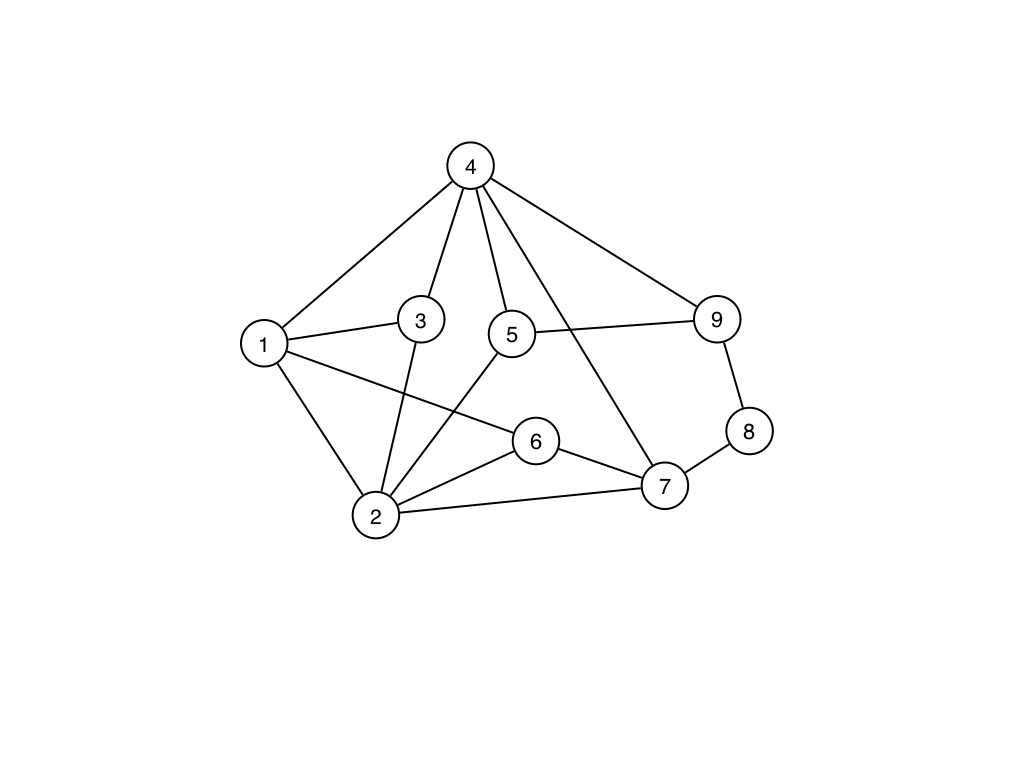
このグラフはchordalではないので，PEOを持ちません．なので，MCS順序も当然PEOではありません． ここで，頂点4から頂点6まで，$P = (4, 1, 2, 6)$というchordless pathがあります． このように$v_i$から$v_j \in V_{i + 1}$まで，頂点番号$i$未満の頂点だけを通ってchordless pathを作れることが$\alpha$が PEOではない必要十分条件だという補題です．

ここから証明を始めますが，いつものように，「$\alpha$がPEOではない」を条件$A$， 「ある頂点$v_i$に対して，$v_i$から$v_j \in V_{i + 1}$までの$V \setminus V_{i + 1}$を通る長さ2以上のchordless pathが存在する」を条件$B$として証明を始めていきます．

まずは$A \to B$を証明します． $\alpha$がPEOではないので，ある頂点$v_i$が存在して，$G[V_i]$中の$N[v_i]$からなる誘導部分グラフはcliqueにはなりません． したがって，$v_i$の隣接頂点に2頂点$v_j, v_k \in V_{i + 1}$が存在し， $v_j$と$v_k$は隣接していません． ここで，一般性を失わずに$id(v_j) < id(v_k)$と仮定できます． $v_j, v_k \in V_{i + 1}$より，$id(v_i) < id(v_j) < id(v_k)$が成り立つので，パス$(v_j, v_i, v_k)$は $v_j$から$v_k \in V_{j + 1}$までの，$V \setminus V_{j + 1}$を通る長さ2のchordless pathになります． よって$A \to B$が成り立ちました．

次に$B \to A$を証明します． $B$の条件を満たすchordless pathがあるので，そのパスを$P = (v_0, v_1, \dots, v_j)$とします．ここで$j \ge 2$を満たします． 今，$P$中の$v_0$と$v_j$以外の頂点で，$\alpha$で振り直した頂点番号で最小の番号を持つ頂点を$u$とします． すると，この$u$は自身よりも大きな頂点番号を持つ$P$中の頂点$x$と$y$に隣接し，$x$と$y$の間に辺はありません． なぜなら，$P$はchordless pathだからです． このとき，$G[V_{id(u) + 1}]$上で$N[u]$はcliqueになりません． したがって$\alpha$はPEOになりません．これで$B \to A$の証明完了です． これで$A \iff B$が証明できました．

ここから$G$がchordalの場合，任意のMCS順序がPEOになる証明に入ります． 興味ある人は是非読んでみてください．

chordal graph $G$の全てのMCS順序は$G$のPEOである．

MCS順序は複数あり得るのですが，ここではその全てがPEOであることを示します． 背理法を用いて証明します．なので，複数あるMCS順序の中でPEOでないMCS順序$\alpha$が存在すると仮定して， $\alpha$はMCSで出力される順序と矛盾することを示します． $\alpha$はPEOではないので，先ほどの補題からある頂点$v_0$を持ち， 長さ2以上のchordless path $P = (v_0, \dots, v_k)$を持ちます．

このような$P$は複数あることが考えられるのですが， ここでは，いくつかある$P$の中で$id(v_0)$が最大な$P$を考えます． ここで，$\alpha$がMCS順序に矛盾することを示したいので， $V \setminus V_{id(v_0) + 1}$中に 次の条件$(1)$を満たす$w$があることを示して証明します．

• $\size{N(v_0) \cap V_{id(v_0) + 1}} < \size{N(w) \cap V_{id(v_0) + 1}} \cdots (1)$

MCSは$V \setminus V_{id(v_0) + 1}$の頂点から$V_{id(v_0) + 1}$に対する次数が大きい頂点を貪欲に取るアルゴリズムなのに， $id(v_0)$よりも小さい頂点番号を持つ$w$が$(1)$を満たすのは アルゴリズムの動作と矛盾します． そこで，今からは$P$中の$v_{k - 1}$が次の条件を満たすことを示します． そのために，以下の条件が成り立つことを示します．

• $N(v_0) \cap V_{id(v_0) + 1} \subset N(v_{k - 1}) \cap V_{id(v_0) + 1}$ $\cdots$ (2)

この条件を満たせば明らかに$id(v_{k - 1}) < id(v_0)$はMCS順序に矛盾します． まず自明な場合を考えます．ここで，長さ1以上のchordless path $P = (v_0, \dots, v_k)$があります． $P$は長さ1以上のchordless pathの中で$id(v_0)$が最大なchordless pathです． $N(v_0) \cap V_{id(v_0) + 1} = \emptyset$の場合， $v_{k - 1}$は$v_k \in N(v_{k - 1}) \cap V_{id(v_0) + 1}$を満たすので， 明らかに$(2)$を満たします．

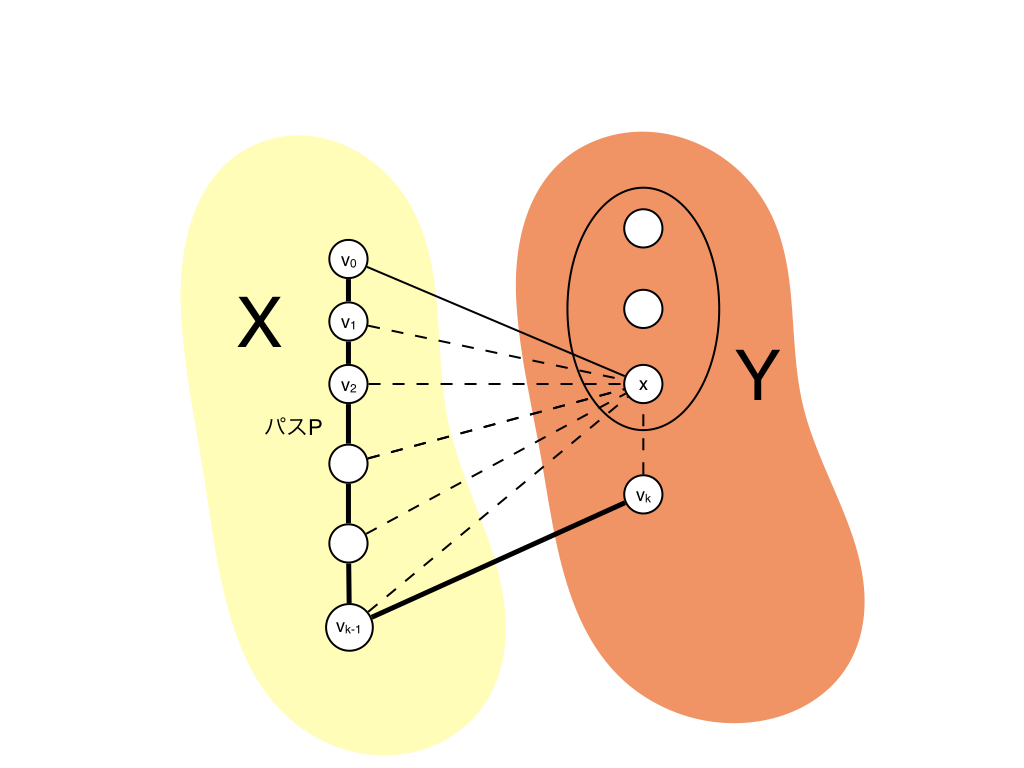
次に$N(v_0) \cap V_{id(v_0) + 1} \neq \emptyset$の場合を考えます． ここで，$x \in N(v_0) \cap V_{id(v_0) + 1}$とし， パス$P' = (x, v_0, \dots, v_k)$を考えます．$P$は$id(v_0)$が最大なchordless path， かつ$id(v_0) < id(x)$なので$P'$はchordを持つパスになります． $P$はchordless pathなので，$P'$の持つchordは$x$と隣接した辺になります． このときもつchordを$e = \set{x, y}$とすると， パス$P'' = (x, y = v_r, \dots, v_k)$が存在するのですが，これも$id(v_0)$の最大性より chordを持つパスになります．さらに，サイクル$C = (x, v_0, \dots, v_r = y, x)$を考えると， $G$がchordalであるという条件から$C$もchordを持ちます． このように，$x$を含むパスやサイクルはchordを持つため， どんどん短いパスやサイクルに分割ができます． この分割を繰り返すと，$P$中のすべての頂点は$x$と辺を持つことがわかります． （下の図のようになります．） つまり，$v_{k - 1}$は$x$と隣接します．したがって，$N(v_0) \cap V{id(v_0) + 1}$中の 任意の頂点は$v_{k - 1}$と隣接します．さらに， $v_0$は$P$がchordless pathであることから$v_k$と隣接せず， $v_{k - 1}$は$v_k$と隣接するので，$(2)$が証明できました． したがって，$G$がchordalの場合，$\alpha$は長さ2以上のchordless pathを持ちません． つまり，MCS順序はPEOになります． サイクルやパスで$P$が短くなっていくのは下の図のようになっています． 太線が$id(v_0)$が最大の誘導パス$P$を表し， 点線は$P$の$id(v_0)$の最大性と$G$がchordalであることから 存在することが証明できる辺です．

終わりに

これで，グラフがchordal graphかどうかを確かめる問題が線形時間で解けることがわかりました． 正当性の証明はそこそこ重い内容でしたが，とりあえず動きを知りたいという人にとっては MCSのアルゴリズム自体は簡単めかと思います．

余談ですが，今回のような「このグラフってhogehoge graphなの？」というYes/No問題のことをgraph recognitionと言います． なので，chordal graphのgraph recognitionは線形時間で解けるということですね！ あとはchordal graphってhyper graphのacyclic性を表すグラフクラスだとか，そういう話を 聞くのですが，ちゃんとはわかっていないので，気になっているところです．（気が向いたら勉強してブログに書くかも？）

次回はclicque treeについてお話ししようと思いましたが，Lex BFSが今回の内容に入らなかったので，先にそちらを説明します． clique treeは今までで一番面白い内容だと思うだけに先延ばしになってしまい残念... 今回から少しずつ内容が重くなっていくと思いますが，頑張ってわかりやすく書きたいと思うので，何かわからないことがあったら是非質問してください！

Chordal Graph: Perfect elimination ordering

3回目のChordal Graph回です． 知識的にストックがあるのと，始めたばかりでやる気があるので，更新ペースがめちゃくちゃ早いです．

今回はPerfect elimination orderingについて説明します． Perfect elimination ordering (PEO) もchordal graphの重要で面白い性質の一つだと思います． chordal graphのいろんないい性質を見ていると，長さ4以上のサイクルには必ず弦があるという定義って結構狭いグラフクラスを 表しているのかなとか思いますね．

Perfect elimination ordering

Perfect elimination orderingとは頂点の順序付で，次の性質をみたす頂点の順序付のことです． どんな性質かというと，ある順序$\pi = (v_1, v_2, \dots, v_n)$の全ての$v_i$が，$G[V_i]$中でsimplicial vertexである とき，$\pi$をperfect elimination orderingと言います．ここで，$V_i$とは$\set{v_i, v_{i + 1}, \dots, v_n}$からなる頂点集合です． 図にするとこんな感じの順序付ですかね．simplicial vertexについてはこちらを見るとわかると思います．

こんな感じに順序付けると確かにどの頂点を見ても自分より頂点番号が大きい頂点からなる誘導部分グラフを考えると自分自身はsimplicial vertexになっていますね． PEOについてはこんな定理が知られています．

$G$がchordalである．$\iff$ $G$がPEOを持つ．

はい，またもや非自明感満載の定理が出てきました． とはいえ，実は前回のsimplicial vertexをうまいこと使うとこの定理も簡単に証明できます． ここでは$G$がchordalという条件を$A$，$G$がPerfect elimination orderingを持つという条件を$B$とします． それでは証明をしていきます． まずは$A \to B$から証明していきます． これは簡単で，前回にやった定理を使うと$G$はsimplicial vertexを1つは持つので，その頂点$v$を$G$から取り除きます． $G \setminus \set{v}$も同様にchordalなので，$G$がなくなるまでsimplicial vertexを選んで行けばPEOができます．

次に$B \to A$を証明します． ここで$\alpha = (u_1, \dots, u_n)$をPEOとします．ここで，$G$にサイクルがないと自明に$G$はchordalなので， $G$はサイクルを持っていると仮定し，その任意のサイクルを$C = (w_1, \dots, w_k)$とします． ここで，頂点番号を$\alpha$の順序で振り直したと考えます．$C$中の番号最小な頂点を$w_i$とすると， PEOの定義より，$w_i$の隣接頂点で，$w_i$より番号の大きな頂点たちはcliqueになっています． すると$C$は弦を持つことになります．また，その弦を含む$C$より短いサイクル$C'$を考えても 同様に頂点番号最小の頂点を持ってくると$C'$は弦を持ちます．これはサイクル長が3になるまで繰り返し 適用できるので，どんな長さ4以上のサイクルを持ってきても必ず弦を持ちます．したがって$G$は chordal graphになります．証明のイメージは下のような感じですかね？

多分次回はMaximum Cardinality Searchの話をして，次の回にClique Treeのことを書こうかと思います． Clique Treeは木幅とかとも関係がある概念だと（僕は）思っています．

雑談

• この辺りは間違ったことを書いている可能性がありますので，変なこと書いていたらごめんなさい．

PEOの存在性もchordal graphの定義になることを紹介しました． 実はPEO繋がりでまだまだ面白い話はあってそれについて少し書いていこうと思います． この論文にも色々書いてありますが， 僕が分かる範囲で書いていこうと思います．

上記の論文中で適当に頂点の順序付をして，その順序付がPEOになるように辺をいくつか追加したグラフを$H$とすると， 元のグラフが$G$がchordalであることと$G$と$H$が一致するような順序付が存在することは 今回示した定理から同値な関係になることがわかります． しかも，PEOは実は線形時間で見つけることができるので，具体的な順序を見つけることも簡単にできます． この線形時間アルゴリズムは2つあって，一つがLexicographic breadth first search（Lex BFS）といい， もう一つが次の回で紹介するMaximum Cardinality Searchというアルゴリズムです．

ここで，この$H$が入力グラフ$G$と一致する順序を見つける問題をchordal graphでないグラフを入力とした場合を考えてみます． そうすると今回示した定理から当然そのような順序は存在しないので， ちょっと問題を変えてみて$G$に追加する辺の数が最小になるような順序付を見つける問題としてみましょう． 要は$H$の辺数から$G$の辺数を引いた値が最小になるようにしたい問題です． この問題はMinimum Fill-inと呼ばれているNP-完全問題になります． Minimum Fill-inは最適な木分解を求める問題と関連が深い問題のようです． （多分どっちかを解くアルゴリズムがあるとちょっと変更を加えるともう片方も解けるのだと思われる） すみません，どういう関連があるかは正確にわかっていない部分はあります． 一応こんな論文は出ていますね． 実際この論文では最適な木幅とMinimum Fill-inを計算するアルゴリズムを与えています． 当然多項式時間アルゴリズムではありませんが． このあたりの問題がにているなぁと感じる理由は後々書きます． もしかしたらそれまでにきちんと勉強して関連の部分を正確に書く日が来るかもしれません．

Chordal Graph: Simplicial vertex

なんか意外に反響があった（アクセスログを見ていたらみんなが見ていてくれた）のでやる気を出したのと，少し今回の内容が簡単だったのもあって が〜っと書いてしまいました．2回目のChordal Graph回です． 今回は次回にやる予定のPerfect elimination orderingのための準備として， Simplicial vertexについて説明していこうかと思います．

Simplicial vertexとは

Simplicial vertexとはすごく単純で，グラフ$G$中で$G[N[v]]$がcliqueになる頂点$v$のことです． 図に書くとこんな感じですね．（$N[v]$は$v$の隣接頂点と$v$からなる集合を表します．） 下の図では頂点$v$は隣接頂点$1, 2, 3$がclicqueになっているのでsimplicial vertexになります．

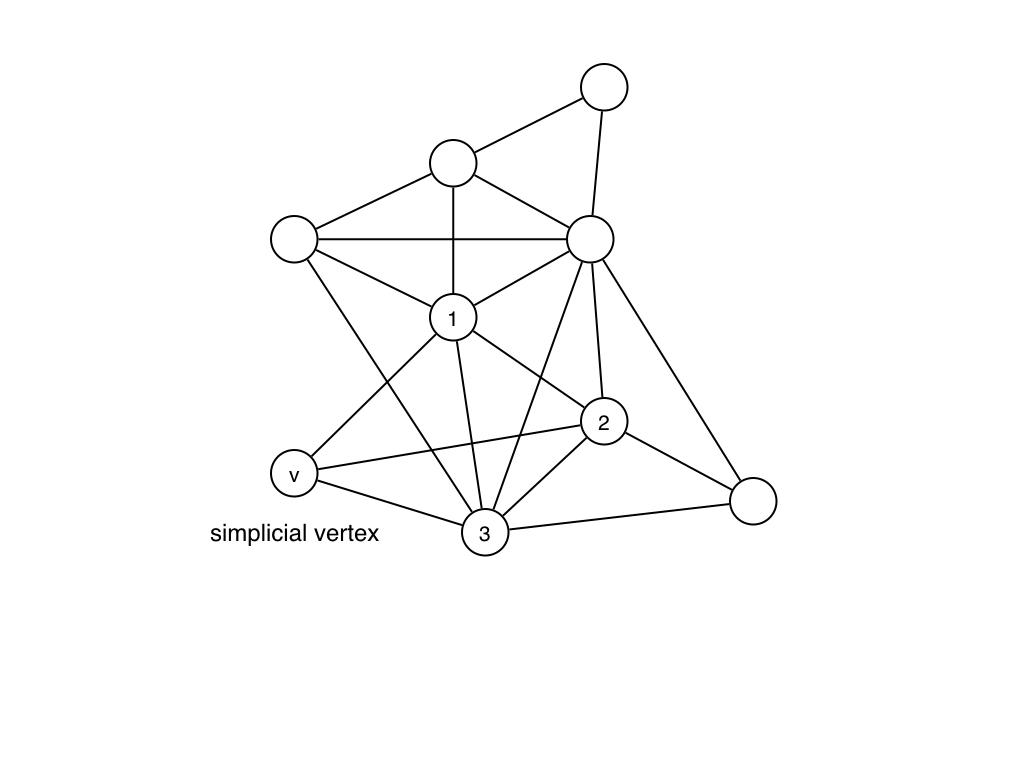
さあ，これがchordal graphとどういう関係があるのかというと，次の定理が知られています．

$G$がchordal graph，かつcomplete graphではない． $\to$ $G$は少なくとも2つの隣接しないSimplicial vertexを持つ

以前紹介した定理よりは少し直感的に正しそうな定理ですね（個人的な感想）． それでは証明していきます．

今回は頂点数に関する数学的帰納法で証明します． 頂点数$2$の場合はグラフは2つしかなくて，頂点$u, v$間に辺がある場合とない場合の2つのグラフしかありません． 辺があるとcomplete graph，辺がない場合は$u$と$v$がsimplicial vertexなので，この定理は成り立ちます． なので，頂点数$k$のchordal かつ completeでない全てのグラフは定理を満たすと仮定します． なので，頂点数$k + 1$の任意のchordal かつ completeでないグラフ$G$を考えます． $G$中の隣接しない2頂点$u, v$を取ってきて，その2頂点をseparateするminimal separatorを$S$とします． このとき，$G$がchordalなので，$S$はcliqueになります．（前回の記事に証明があります） さらに，$S$がseparatorなので，連結成分$A$と$B$が$G \setminus S$中に存在します． ここで，$u \in A$，$v \in B$としても一般性を失わないのでそう仮定します． したがって，$A \neq \emptyset$かつ$B \neq \emptyset$となります． $G[A \cup S]$と$G[B \cup S]$を考えると，この2つは$\size{G[A \cup S]}, \size{G[B \cup S]} < \size{G}$を満たします．

$G$の誘導部分グラフはchordalなので，$G[A \cup S]$と$G[B \cup S]$がcompleteでないならば， 帰納法の仮定より，simplicial vertexを2つずつ持つことになります． さらに，$G[A \cup S]$中のsimplicial vertexを2頂点$x, y$とすると， $x, y$は隣接しません．したがって，$x$か$y$のどちらかは$S$に含まれていません． なぜなら$S$はcliqueだからです．ここで，$S$に含まれる頂点を$x$とします． すると，$y$は$A$に含まれ，$G[A \cup S]$中の$y$の隣接関係と $G$中の$y$の隣接関係は一致します． したがって，$y$は$G$中でもsimplicial vertexになっています． また，$G[A \cup S]$と$G[B \cup S]$がcompleteだったとしても， それらのグラフは$S$に含まれないsimlicial vertexは必ず1つは持ち， その2つの頂点は元のグラフで隣接していないので，$G$は隣接していない2つのslimlicial vertexを持ちます． よって証明終了です． 証明のイメージ図はこんな感じですね．

$G$を2つに分割するんですが，そうすると$G$よりサイズの小さい2つのグラフができて，その2つのグラフはchordalだし，たとえcompleteだとしても1つは $S$に含まれないsimplicial vertexを持つので，隣接しない2つのsimplicial vertexはあるよね！という証明です． ただし，図中の$x$のように分割後の$G[A \cup S]$や$G[B \cup S]$中でsimplicialだとしても元のグラフ$G$ではsimlicialではない頂点もあります． そういう頂点を考慮しても隣接しない2つのsimplicial vertexがchordal graph$G$中には存在します．

今回の内容は少し軽めでしたが， すみません，以前の証明は間違いがありました． 現在は修正されています．（11/06）

この定理はこれからの証明にすごく便利なので， 僕としては後になればなるほどいい性質だなぁと感心しました．