Chordal Graph: Simplicial vertex

なんか意外に反響があった（アクセスログを見ていたらみんなが見ていてくれた）のでやる気を出したのと，少し今回の内容が簡単だったのもあって が〜っと書いてしまいました．2回目のChordal Graph回です． 今回は次回にやる予定のPerfect elimination orderingのための準備として， Simplicial vertexについて説明していこうかと思います．

Simplicial vertexとは

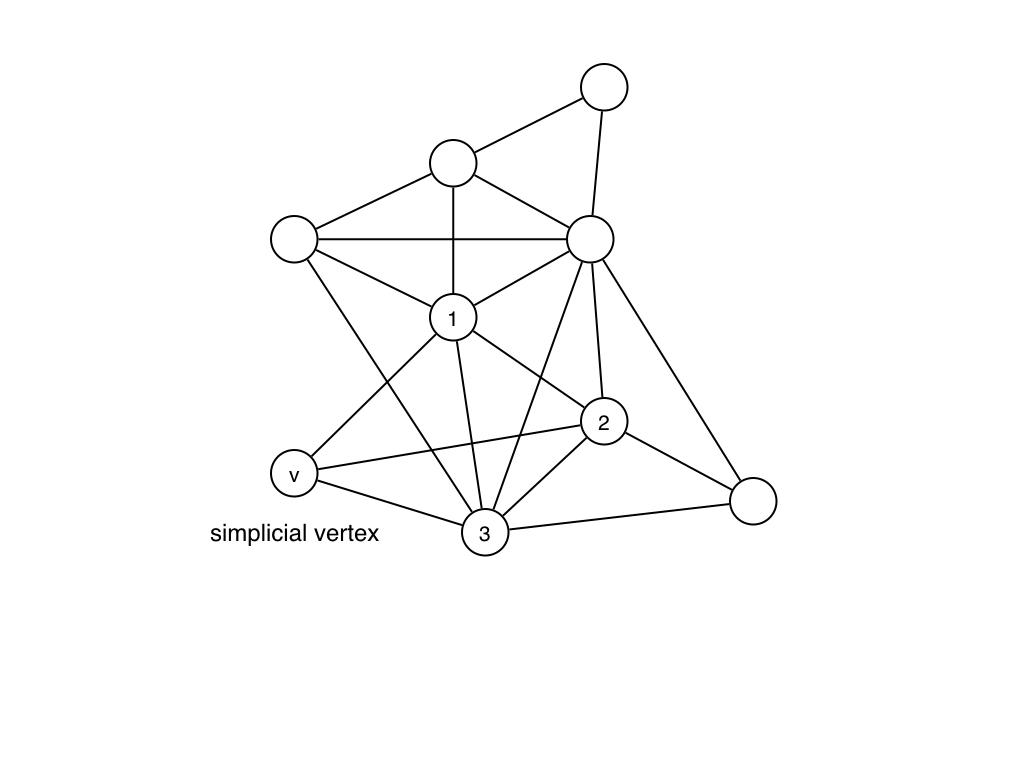
Simplicial vertexとはすごく単純で，グラフ$G$中で$G[N[v]]$がcliqueになる頂点$v$のことです． 図に書くとこんな感じですね．（$N[v]$は$v$の隣接頂点と$v$からなる集合を表します．） 下の図では頂点$v$は隣接頂点$1, 2, 3$がclicqueになっているのでsimplicial vertexになります．

さあ，これがchordal graphとどういう関係があるのかというと，次の定理が知られています．

$G$がchordal graph，かつcomplete graphではない． $\to$ $G$は少なくとも2つの隣接しないSimplicial vertexを持つ

以前紹介した定理よりは少し直感的に正しそうな定理ですね（個人的な感想）． それでは証明していきます．

今回は頂点数に関する数学的帰納法で証明します． 頂点数$2$の場合はグラフは2つしかなくて，頂点$u, v$間に辺がある場合とない場合の2つのグラフしかありません． 辺があるとcomplete graph，辺がない場合は$u$と$v$がsimplicial vertexなので，この定理は成り立ちます． なので，頂点数$k$のchordal かつ completeでない全てのグラフは定理を満たすと仮定します． なので，頂点数$k + 1$の任意のchordal かつ completeでないグラフ$G$を考えます． $G$中の隣接しない2頂点$u, v$を取ってきて，その2頂点をseparateするminimal separatorを$S$とします． このとき，$G$がchordalなので，$S$はcliqueになります．（前回の記事に証明があります） さらに，$S$がseparatorなので，連結成分$A$と$B$が$G \setminus S$中に存在します． ここで，$u \in A$，$v \in B$としても一般性を失わないのでそう仮定します． したがって，$A \neq \emptyset$かつ$B \neq \emptyset$となります． $G[A \cup S]$と$G[B \cup S]$を考えると，この2つは$\size{G[A \cup S]}, \size{G[B \cup S]} < \size{G}$を満たします．

$G$の誘導部分グラフはchordalなので，$G[A \cup S]$と$G[B \cup S]$がcompleteでないならば， 帰納法の仮定より，simplicial vertexを2つずつ持つことになります． さらに，$G[A \cup S]$中のsimplicial vertexを2頂点$x, y$とすると， $x, y$は隣接しません．したがって，$x$か$y$のどちらかは$S$に含まれていません． なぜなら$S$はcliqueだからです．ここで，$S$に含まれる頂点を$x$とします． すると，$y$は$A$に含まれ，$G[A \cup S]$中の$y$の隣接関係と $G$中の$y$の隣接関係は一致します． したがって，$y$は$G$中でもsimplicial vertexになっています． また，$G[A \cup S]$と$G[B \cup S]$がcompleteだったとしても， それらのグラフは$S$に含まれないsimlicial vertexは必ず1つは持ち， その2つの頂点は元のグラフで隣接していないので，$G$は隣接していない2つのslimlicial vertexを持ちます． よって証明終了です． 証明のイメージ図はこんな感じですね．

$G$を2つに分割するんですが，そうすると$G$よりサイズの小さい2つのグラフができて，その2つのグラフはchordalだし，たとえcompleteだとしても1つは $S$に含まれないsimplicial vertexを持つので，隣接しない2つのsimplicial vertexはあるよね！という証明です． ただし，図中の$x$のように分割後の$G[A \cup S]$や$G[B \cup S]$中でsimplicialだとしても元のグラフ$G$ではsimlicialではない頂点もあります． そういう頂点を考慮しても隣接しない2つのsimplicial vertexがchordal graph$G$中には存在します．

今回の内容は少し軽めでしたが， すみません，以前の証明は間違いがありました． 現在は修正されています．（11/06）

この定理はこれからの証明にすごく便利なので， 僕としては後になればなるほどいい性質だなぁと感心しました．