木の同型性判定のお話
この記事は文字列アドベントカレンダー5日目の記事です.
はじめに
文字列Advent Calendarと言いつつ,木について書いていこうかなと思います. まあ,文字列ガチ勢から見れば,根付き木は実質文字列なので,このCalendarで書いてもみんな喜んでくれると信じています. あと,実際ここで紹介する手法でも木を文字列に変換してから色々やって,木の同型性を判定します.
紹介内容
今回紹介するのはタイトル等にもあるように,木の同型性判定問題を線形時間で解くアルゴリズムの紹介をします. 木のお話をする前にグラフの同型性判定問題について説明します.グラフの同型性判定問題とは,2つのグラフ$G$と$H$が与えられた時,$G$と$H$の頂点間に辺の有る無し関係を変えないような頂点の対応付けがありますか?というYes/No問題に答える問題です. 木の同型性判定問題とは,この入力グラフ$G$を木に限定した場合にどうやったら解けるの?という問題です.
根付き木の同型性判定問題
いきなり木に限定するとよくわからないので,根付き木の同型性判定から紹介しましょう. 以下この節の説明では木といったら根付き木と思ってください. この内容はこのPDFと このスライドの内容です. また,スライド中のAHUアルゴリズムは[1]の本の内容です. 僕は本が手に入らなかったので,スライドで勉強しました,
ここでは文字列ガチ勢の人々が大好き(と思われる)テクニックである,木の文字列への変換を使います. 木の同型性判定のアルゴリズムの概要をざっくり説明すると,木をあるルールで文字列にして,
- 変換後の2つの文字列が同じである $\iff$ 2つの木が同型である
という変換ルールを与えるというアルゴリズムです. 木を括弧列に変換する方法は簡単で,次のように変換します.

これは葉を"()"とし,中間ノードは子供を1列に並べて両端を"("と")"でまとめるといった操作で 木を文字列に変換します.中間ノードに対応する文字列を生成する場合,子供の文字列をソート順で 連結するようにします.結論から言うと, 実はこの文字列が一致していることと木が同型であることが同値な条件になっています. 以降はこの正当性についてて見ていきます. 正当性のきちんとした証明を見ようと上記のスライドと資料を見たら"明らかである.","証明は簡単だ"と書かれていました. 悲しい... ゆるふわに証明らしき物を考えてみます. まずは
* 括弧列が同じである $\to$ 木が同型である.
ですが,こちらは問題なく正しそうに見えます.次に
- 木が同型である $\to$ 括弧列が同じである.
を考えてみます. これは正しそうで,帰納的に考えると, 高さ$0$の木は自明に同型ならば括弧列が同じになります. 高さ$k$以下の木は正しく括弧列が同じくなるとし, 高さ$k + 1$の木を考えます. この時,根を親に持つ頂点以下のそれぞれの部分木を考えて,それらの部分木を文字列に変換すると, それぞれの部分木は高さ$k$以下なので,木が同型ならば括弧列が同じになります. その括弧列をソートしたとすると,元の木の文字列も一意に定まり, 木が同型ならば括弧列が同じになります. こんな感じに帰納法的に考えるとこの条件が正しい気がして来ます.
次にこのアルゴリズム(以降ではAHUアルゴリズムと言います.これはAho,Hopcroft,Ullmanの頭文字から来ています.) の時間計算量を考えます.これは最悪ケース各ノード $O(n)$ 文字持つことになるので $O(n2)$ 時間アルゴリズムです. AHUアルゴリズムを線形時間になるように改良します.
と思いましたが,時間の関係上とりあえず割愛します.(気が向いたら更新しときます.) 雰囲気で説明すると下の図のように毎回文字列を整数値1つに書き換えます.
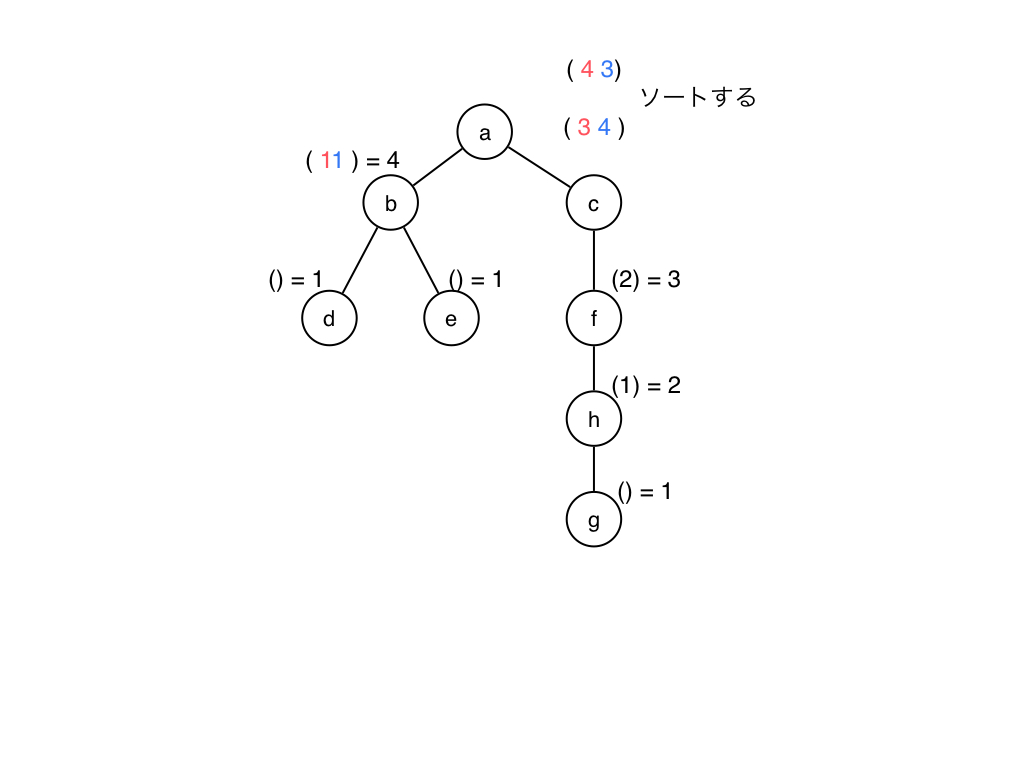
木の同型性判定
先ほど与えた根付き木の同型性判定問題を解くアルゴリズムを使って木の同型性判定を解きましょう. ここで,グラフには中心という頂点が存在します. 中心の説明の前にグラフの半径(radius)について定義します. ここで,$G$中の任意の頂点$u$とした時,$v, u$間の距離を$d(u, v)$と定義します. グラフ$G$中の$v$が$G$の中心であるとは,$max_{u \in V}(d(u, v))$が最小な頂点$v$を$G$の中心と言います. つまり,どんなに遠くに行こうとしても最短パスしか通れないならあんまり遠くに行けない頂点ということです.
そして木が同型なので,
- 木が同型である $\to$ $G$の中心は$H$の中心に対応付けられる
ということがわかります. したがって,同型ならば少なくとも中心は等しくなります. この性質より,根無し木を,木の中心同士を根と思って 根付き木にとし,根付き木の同型性判定アルゴリズムを使えば終わりです. また,木には中心が高々2つしか存在しないので,定数回の AHUアルゴリズムの適用で判定ができます. したがって根無し木も $O(n)$ 時間で同型性が判定可能です.
非常にゆるゆるで申し訳ないですが, こんな感じで木の同型性判定が行えます.
僕は$O(n \log n)$の雑実装でこんな感じで実装しました.
参考文献
- Aho, Alfred V., and John E. Hopcroft. The design and analysis of computer algorithms. Pearson Education India, 1974.