$\newcommand{\set}[1]{\{#1\}}$ $\newcommand{\inset}[2]{\{#1 \mid #2\}}$ $\newcommand{\name}[1]{\emph{#1}}$ $\newcommand{\size}[2][]{\left| #2^{#1} \right|}$ $\newcommand{\sig}[1]{\mathcal{#1}}$

辞書順幅優先探索Lex BFS（Chordal Graph 5回）

この記事はデータ構造とアルゴリズムアドベントカレンダー 2018の19日目の記事です．

qiita.com

とりあえず懺悔します．遅れて申し訳ありません．

データ構造とアルゴリズムアドベントカレンダーで列挙とかの話をしようかなぁとか思ったのですが，書くのが大変だったのと， これ読みそうな人類って誰だ？という気持ちになったので，ちょっと違う話をしようと思います． なので，今回は探索アルゴリズムの基本とも言える幅優先探索の亜種である辞書順幅優先探索について書いていきます． （ちなみにこの記事は1年くらい更新していなかったChordal Graphの第5回も兼ねています．） 今回のネタ本はこんな感じです． Graph Classes: A Survey Algorithmic Graph Theory and Perfect Graphs

グラフ探索アルゴリズム

有名なグラフ探索アルゴリズムとして幅優先探索（breadth first search, BFS）と深さ優先探索（depth first search）があります． これらは（多分）情報系の大学に行くと2年生か3年生くらいに習って，多分授業で実装をする機会もあるくらい有名なアルゴリズムだと思います． しかも，これらのアルゴリズムはグラフ探索だけでなく，メモリと時間を気にしさえしなければ（指数時間，指数メモリを許せば）いろんな問題がこの2つの探索で解くことができます． グラフ探索っぽくない幅優先探索の使い方でよくあるのは次のような問題ですかね？

  • 15パズルを完成させる最短手数を求めよ

これらのグラフ探索アルゴリズムは簡単ですが，実は使い勝手が良く，いろんな問題がDFSやBFSっぽい考えで解くことができます．

  • グラフ上の最短経路問題: BFS
  • グラフ上の最短閉路問題: BFS
  • グラフの平面性判定: DFS
  • 関節点や橋の列挙: DFS
  • 有向グラフの強連結成分分解: DFS

（何か他にいい例を知っている方がいたら教えてください．．．）

そんなBFS，DFSの中で，今回は少し変わったBFSであるLex BFS（Lexicographical BFS）を紹介しようと思います． これはほぼBFSと同じなんですが，キューに次の頂点を追加する際，少しだけ追加の順序が異なります． 通常のグラフ探索のBFSする場合，ある頂点$v$をみて，$v$の隣接頂点をキューに追加する順番は適当で良いのですが， Lex BFSではちょっと頭を使ってキュー中の順序を管理します．

Lex BFS

Lex BFSの疑似コードは次のようになります．まずは前提として，$G$中の任意の頂点$v$は1つの文字列$S_v$を持っていると思ってください． 初期値として$S_v = \emptyset$とします．また，以下では数字を文字のように扱います．文字列は数字の列だと思ってください．

$LexBFS(G)$ 入力: グラフ$G$，頂点数 $n$ ，辺数 $ m $

  1. $G$の任意の頂点$v$は文字列$S_v = \emptyset$を持ちます．
  2. $G$中の頂点で辞書順最大の文字列を持つ頂点$v$を選ぶ．（もし辞書順最大が複数ある時はその中から任意に選んで良い．）
  3. $v$の隣接頂点$u$が持つ$S_u$の末尾に文字$n$を追加します．
  4. $n$を1つ小さくして，2行目の処理に飛びます．

実行例はこんな感じです．

f:id:chocobaby-aporo:20181225010348g:plain

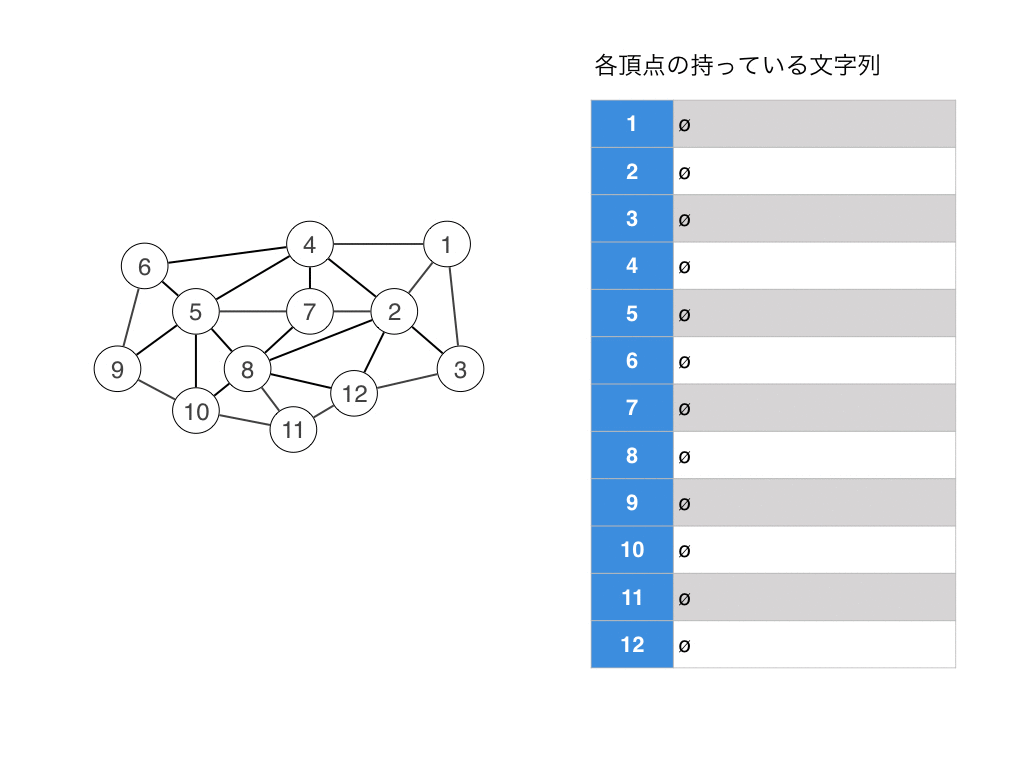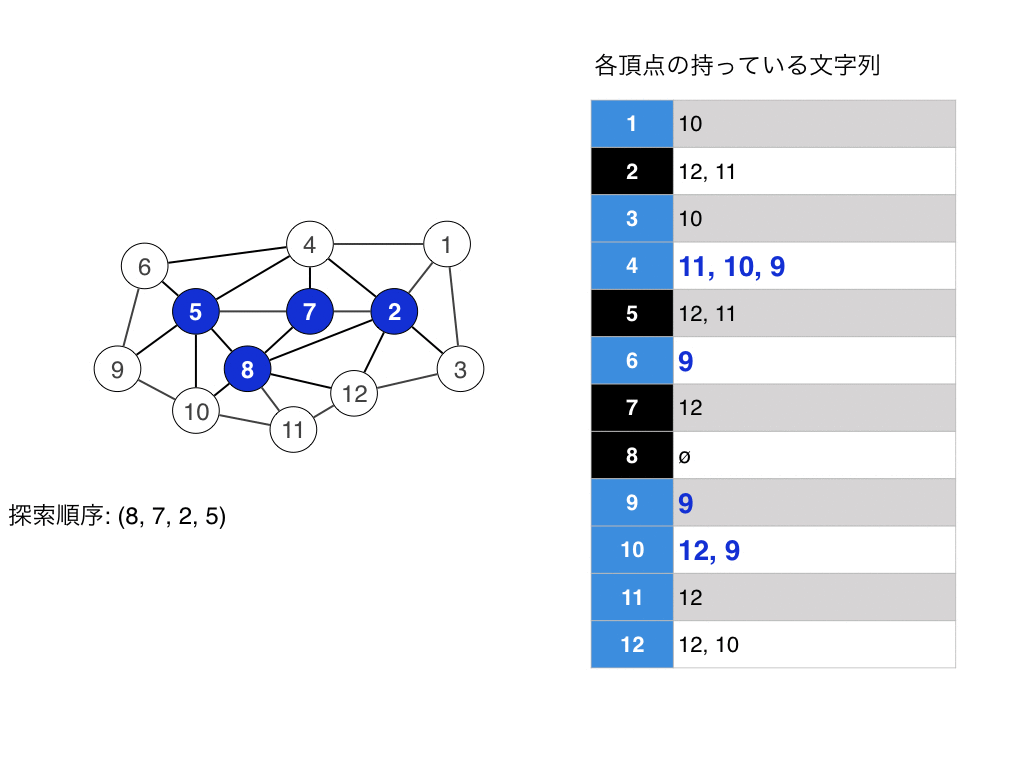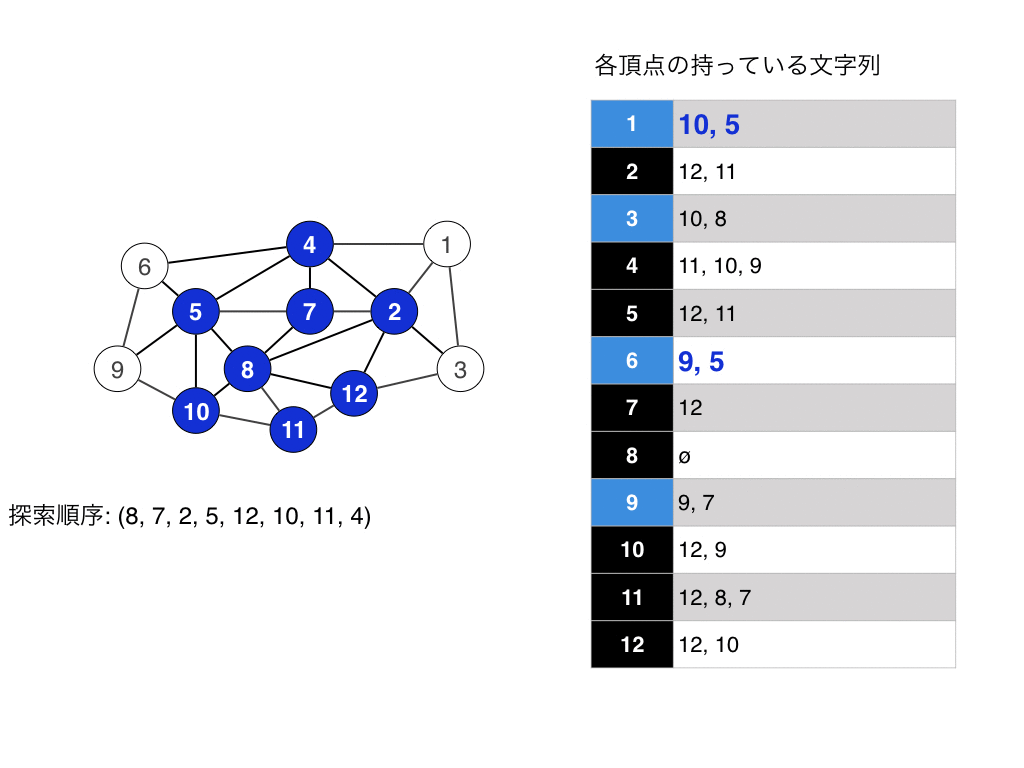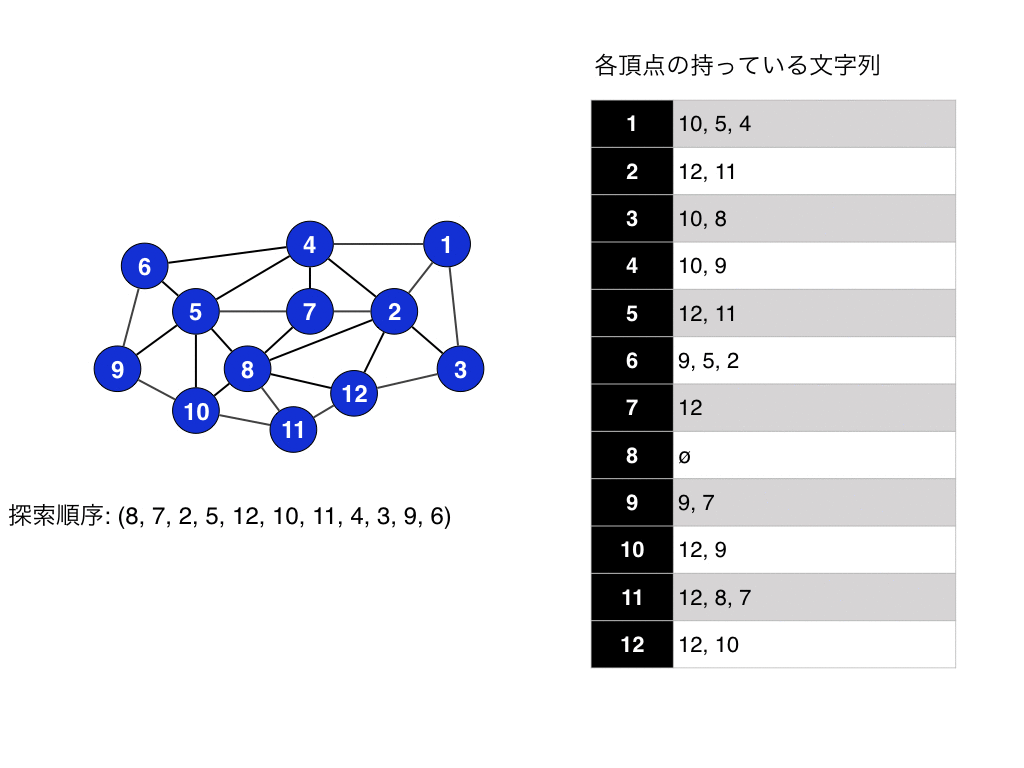
実はLexBFSはコーディングを頑張ると線形時間で実装できます． 実装をwikiを見るとなんとなくわかると思います． 簡単にいうとリストと$n$個の番兵的なものを使うと実装できると思います．

Lex BFSを用いたグラフのChordality判定

実はこのLexBFSを使ってグラフがchordal graphかどうかの判定問題が解けます． 方法は簡単で，Lex BFSをして求めた頂点の探索順の逆順がPerfect elimination ordering (PEO)かどうかを確かめるだけです． 実際に(8, 7, 2, 5, 12, 10, 11, 4, 3, 9, 6)の順序を逆にした(6, 9, 3, 4, 11, 10, 12, 5, 2, 7, 8) は入力グラフ$G$のPEOになっています． ここで，PEOの定義は次の通りです．頂点順序$σ = (v_1, v_2, ..., v_n)$が任意の$v_i$に対して，$v_i$から$v_n$を用いて作る誘導部分グラフ$G'$の中で$v_i$がsimplicial vertexであるとき，$σ$をPEOと言います．また，ある頂点$v$がsimplicial vertexであるとは，$v$とその隣接頂点からなる誘導部分グラフがクリークになることを言います．

では，この順序がきちんとPEOになっていることを証明してみます． と思ったのですが，本当に申し訳ありませんが，証明はもう少し後に公開します． （完全に理解していない + 時間が足りない）

　LexBFSの他の使い道

LexBFSは他にも使い道があって，次のグラフクラスの認識にも使えるようです．

  • HHD-free graph
  • distance-hereditary graph
  • interval graph
  • co graph graph

この辺りのこともいつか書いて見たいですね．