Chordal Graph: Maximum Cardinality Search

今回はグラフの性質のお話ではなくPEOを求めるためのアルゴリズムのお話をします． MCSとLex BFSというアルゴリズムのお話をします． chordal graphの性質についてはこの2つのアルゴリズムを説明した後にもまだまだ書きます．

今回は長くなるので，2回に分けました． PEOを求めるアルゴリズムだけ知りたい人は今回のMCSの部分だけ読むとわかると思います． ただ，Lex BFSはMCSよりも便利な印象があって，Lex BFSを使うと他の問題も解けるようです． 例としてあげられるのは1つしか知りませんが，入力グラフ$G$がCo-graph($P_4$-free graph)，つまり， 誘導部分グラフとして長さ4のパスを含まないグラフかどうかの判定問題もLex BFSで解けるらしいです． 論文とかではなく，ネット上の資料ですが，こんなスライドがあって，紹介されています． 多分競プロerなら知っていると思いますが，hosさんのスライドです． こちらはブログでは紹介しなさそうな予感です．気が向いたらするかも？

今回のお話に入っていきます．前回PEOという順序があることとグラフがchordalであることが同値であることはわかりました． でもPEOを計算できないとグラフがchordalかどうかを確かめられないので悲しい気持ちになります． しかし，PEOはグラフサイズに対して線形時間で求めるMCSとLex BFSという2つのアルゴリズムがあります． 今回はそのうちの1つのMCSを紹介します．Lex BFSは次回説明するのでお楽しみに！

Maximum cardinality search

まずはアルゴリズムの動きを説明した後で，アルゴリズムの正当性を証明します． 計算時間の解析はほぼ自明なので，特にはしません． MCSは，単純にいうと貪欲に次数の大きい頂点から頂点をとっていくだけのアルゴリズムなのですが， どういったグラフの中で次数が大きいのかを考えるのがキモになります．当然ですが，入力グラフ$G$を 考えて，そこから次数の大きい順に頂点を選んで順序付してもPEOにはなりません．

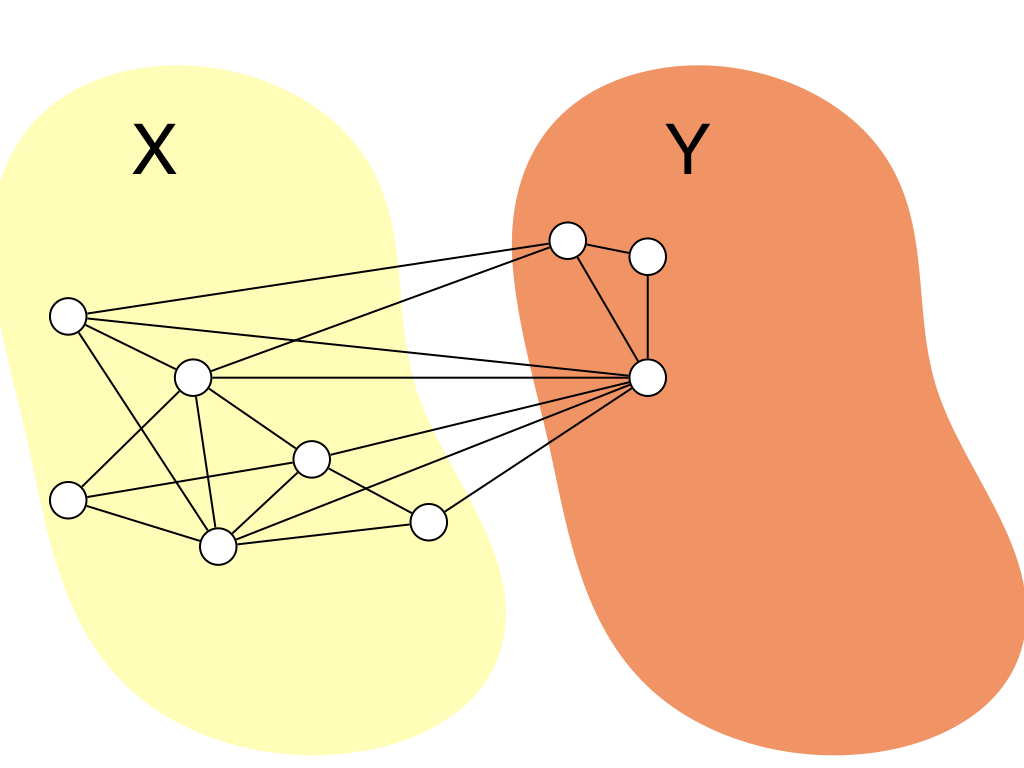
そこで，入力グラフ$G = (V, E)$に対してどういったグラフを考えるかというと， 二部グラフっぽいグラフ？$H = (X, Y, E)$を考えます． ここで，$H$は，$X \cup Y = V$かつ$X \cap Y = \emptyset$を満たします．辺集合は$G$と$H$は同じです． $X$間の2頂点や$Y$間の2頂点にも辺はあるので，二部グラフではないのですが，それに近いイメージです． つまりは頂点集合を2つに分割したグラフを考えるということですね．図にするとこんな感じです．

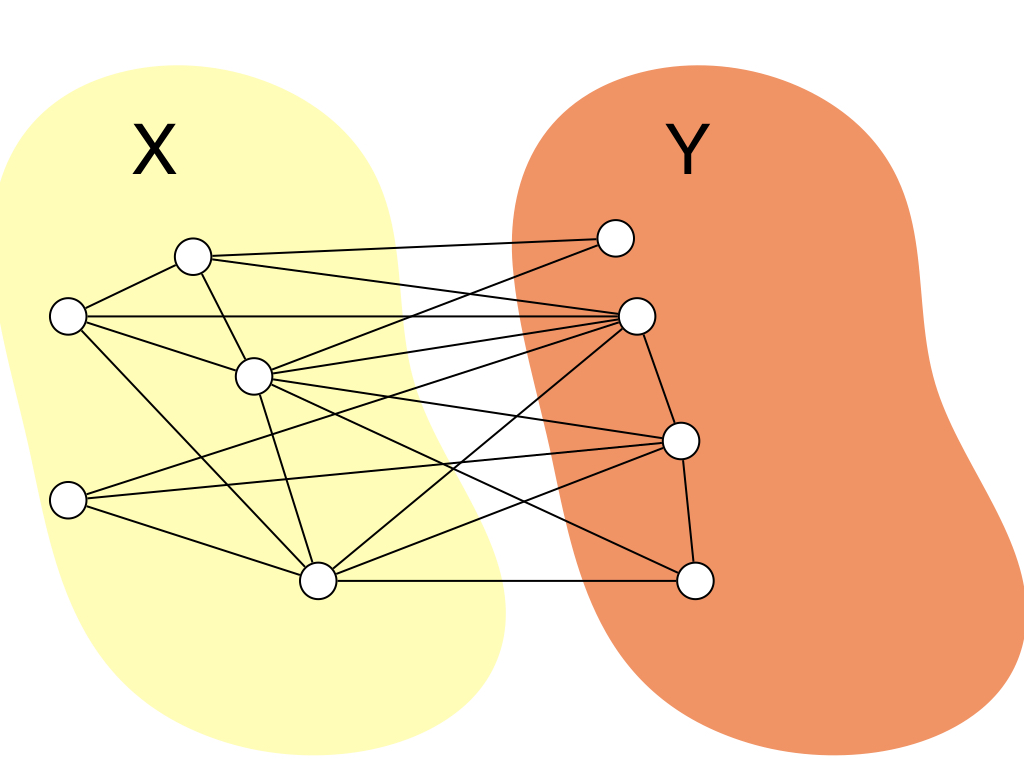
$H$は初期状態として，$X = V$，$Y = \emptyset$を満たすとします．ここで，$\size{N(v) \cap Y}$が最大になるような 頂点$v \in X$を選択します．また，$\size{N(v) \cap Y}$の値が同じ$v$が複数ある場合はそのうちの任意の1つを選択します． そして，$v$を$X$から$Y$に移動させます．つまり$H' = (X \setminus \set{v}, Y \cup \set{v}, E)$というグラフに更新します． これを$X$が空集合になるまで繰り返します． すると，グラフがchordalであれば必ずこの頂点の追加順の逆順がPEOになります． 証明は後で行います． ここでは，順序付の逆順をMCS順序と呼ぶことにします． ただし，この順序はchordal graphでなくても定義できるので，本当にMCS順序がPEOになっているかはチェックする必要はあります． ここで保証されるのは，$G$がchordalであればMCS順序が必ずPEOになるということ保証します． アルゴリズムの動きはこんな感じですね．

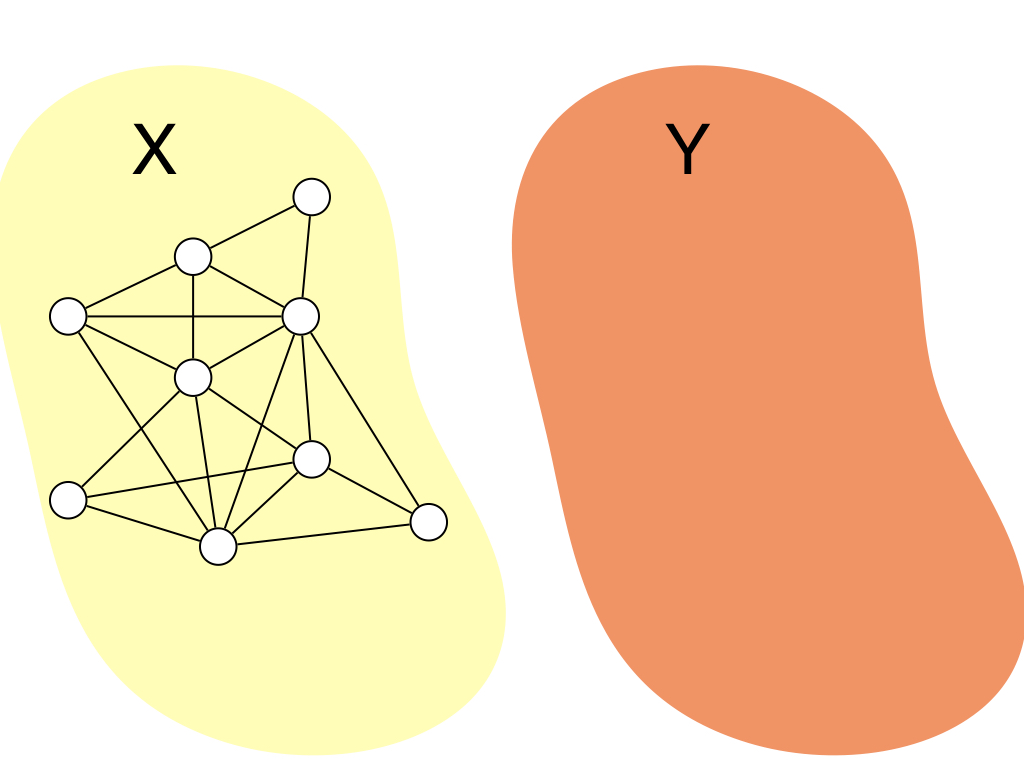
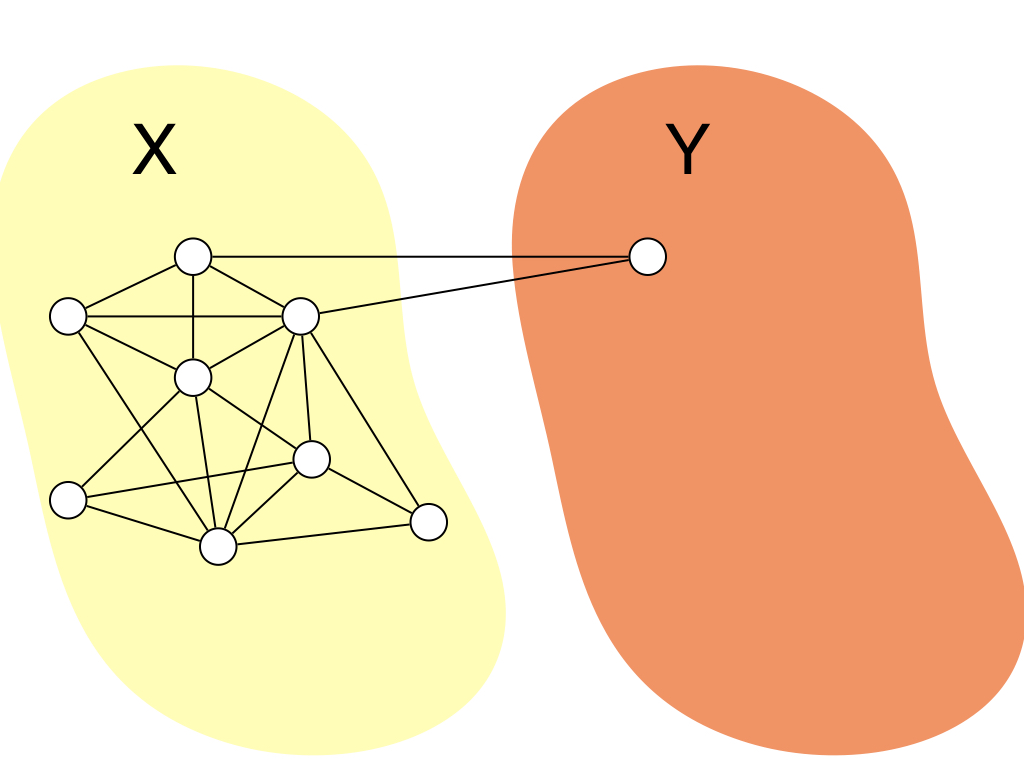
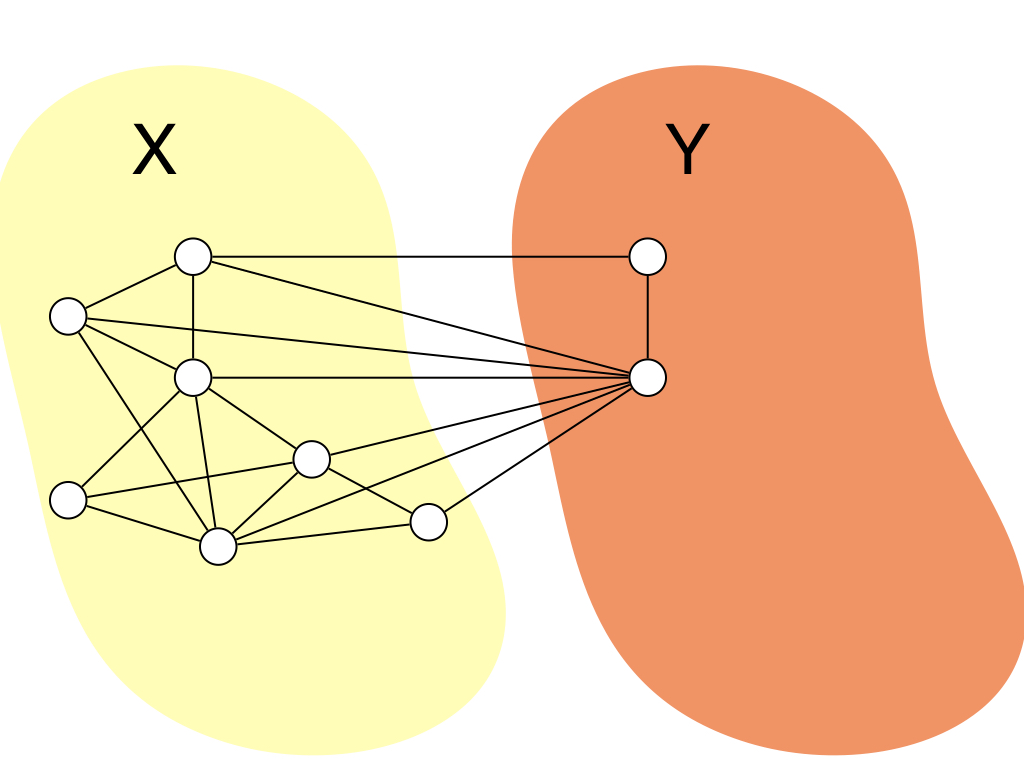
ついでに大雑把に計算時間についていうと，このアルゴリズムを線形時間で実装する方法は色々あると思うのですが， $X$中の頂点集合の次数順ソートした頂点列を持っていて，$X$から$Y$に頂点が移動するたびにそれを更新すれば $O(\Delta)$時間で1つの頂点を移動できるので，全体で$O(n + m)$時間で計算できます．（$n$と$m{}$ は頂点数と辺数） ソートには$O(n \log n)$かかるんじゃね？っと思うかもしれないですが，次数はたかだか$n$しかないので， バケットソートすると線形時間でソートできます．色々自分のやりやすい実装を考えてみてください． （記事を見ている人は競プロerが多い想定なので，いい実装を思いついてくれそう）

MCSの正当性の証明

これ以降は正当性の証明です．ここでは，MCSで作る任意の順序付を$\alpha$とします． これ以降では頂点番号はの順序で番号を振り直したと考えてください． 例えば，頂点数4のグラフがあって，$\alpha = (3, 2, 4, 1)$だったら， 3を1に，2を2に，4を4に，1を4に番号をつけ直したと考えてください． グラフがchordalである場合，この順序が必ずPEOを出力することを証明します． 今回は直接これを証明する前に次の補題を証明します． ここで，$V_i$は頂点番号$i$から$n$までの頂点を含む集合とし， 頂点$v$の頂点番号を$id(v)$と表記することにします．

$\alpha$がPEOではない $\iff$ ある頂点$v_i$に対して，$v_i$から$v_j \in V_{i + 1}$までの$ V \setminus V_{i+1} $を通る長さ2以上のchordless pathが存在する．

chordless pathとはpath $P = (v_1, \dots, v_k)$の任意の頂点$v_i$が$v_{i - 1}$と$v_{i + 1}$以外の頂点と隣接しないpathです． ちょっとこの補題が何を言っているのかわかりにくいと思うので，この補題が表す状態を図にするとこんな感じです．

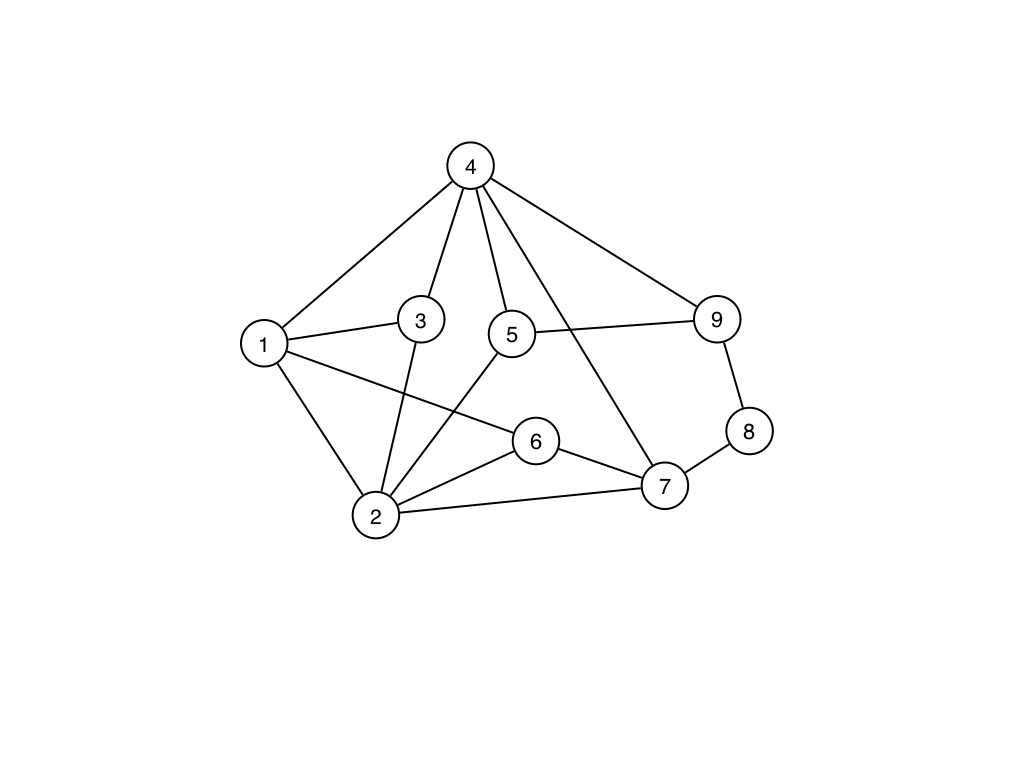
このグラフはchordalではないので，PEOを持ちません．なので，MCS順序も当然PEOではありません． ここで，頂点4から頂点6まで，$P = (4, 1, 2, 6)$というchordless pathがあります． このように$v_i$から$v_j \in V_{i + 1}$まで，頂点番号$i$未満の頂点だけを通ってchordless pathを作れることが$\alpha$が PEOではない必要十分条件だという補題です．

ここから証明を始めますが，いつものように，「$\alpha$がPEOではない」を条件$A$， 「ある頂点$v_i$に対して，$v_i$から$v_j \in V_{i + 1}$までの$V \setminus V_{i + 1}$を通る長さ2以上のchordless pathが存在する」を条件$B$として証明を始めていきます．

まずは$A \to B$を証明します． $\alpha$がPEOではないので，ある頂点$v_i$が存在して，$G[V_i]$中の$N[v_i]$からなる誘導部分グラフはcliqueにはなりません． したがって，$v_i$の隣接頂点に2頂点$v_j, v_k \in V_{i + 1}$が存在し， $v_j$と$v_k$は隣接していません． ここで，一般性を失わずに$id(v_j) < id(v_k)$と仮定できます． $v_j, v_k \in V_{i + 1}$より，$id(v_i) < id(v_j) < id(v_k)$が成り立つので，パス$(v_j, v_i, v_k)$は $v_j$から$v_k \in V_{j + 1}$までの，$V \setminus V_{j + 1}$を通る長さ2のchordless pathになります． よって$A \to B$が成り立ちました．

次に$B \to A$を証明します． $B$の条件を満たすchordless pathがあるので，そのパスを$P = (v_0, v_1, \dots, v_j)$とします．ここで$j \ge 2$を満たします． 今，$P$中の$v_0$と$v_j$以外の頂点で，$\alpha$で振り直した頂点番号で最小の番号を持つ頂点を$u$とします． すると，この$u$は自身よりも大きな頂点番号を持つ$P$中の頂点$x$と$y$に隣接し，$x$と$y$の間に辺はありません． なぜなら，$P$はchordless pathだからです． このとき，$G[V_{id(u) + 1}]$上で$N[u]$はcliqueになりません． したがって$\alpha$はPEOになりません．これで$B \to A$の証明完了です． これで$A \iff B$が証明できました．

ここから$G$がchordalの場合，任意のMCS順序がPEOになる証明に入ります． 興味ある人は是非読んでみてください．

chordal graph $G$の全てのMCS順序は$G$のPEOである．

MCS順序は複数あり得るのですが，ここではその全てがPEOであることを示します． 背理法を用いて証明します．なので，複数あるMCS順序の中でPEOでないMCS順序$\alpha$が存在すると仮定して， $\alpha$はMCSで出力される順序と矛盾することを示します． $\alpha$はPEOではないので，先ほどの補題からある頂点$v_0$を持ち， 長さ2以上のchordless path $P = (v_0, \dots, v_k)$を持ちます．

このような$P$は複数あることが考えられるのですが， ここでは，いくつかある$P$の中で$id(v_0)$が最大な$P$を考えます． ここで，$\alpha$がMCS順序に矛盾することを示したいので， $V \setminus V_{id(v_0) + 1}$中に 次の条件$(1)$を満たす$w$があることを示して証明します．

• $\size{N(v_0) \cap V_{id(v_0) + 1}} < \size{N(w) \cap V_{id(v_0) + 1}} \cdots (1)$

MCSは$V \setminus V_{id(v_0) + 1}$の頂点から$V_{id(v_0) + 1}$に対する次数が大きい頂点を貪欲に取るアルゴリズムなのに， $id(v_0)$よりも小さい頂点番号を持つ$w$が$(1)$を満たすのは アルゴリズムの動作と矛盾します． そこで，今からは$P$中の$v_{k - 1}$が次の条件を満たすことを示します． そのために，以下の条件が成り立つことを示します．

• $N(v_0) \cap V_{id(v_0) + 1} \subset N(v_{k - 1}) \cap V_{id(v_0) + 1}$ $\cdots$ (2)

この条件を満たせば明らかに$id(v_{k - 1}) < id(v_0)$はMCS順序に矛盾します． まず自明な場合を考えます．ここで，長さ1以上のchordless path $P = (v_0, \dots, v_k)$があります． $P$は長さ1以上のchordless pathの中で$id(v_0)$が最大なchordless pathです． $N(v_0) \cap V_{id(v_0) + 1} = \emptyset$の場合， $v_{k - 1}$は$v_k \in N(v_{k - 1}) \cap V_{id(v_0) + 1}$を満たすので， 明らかに$(2)$を満たします．

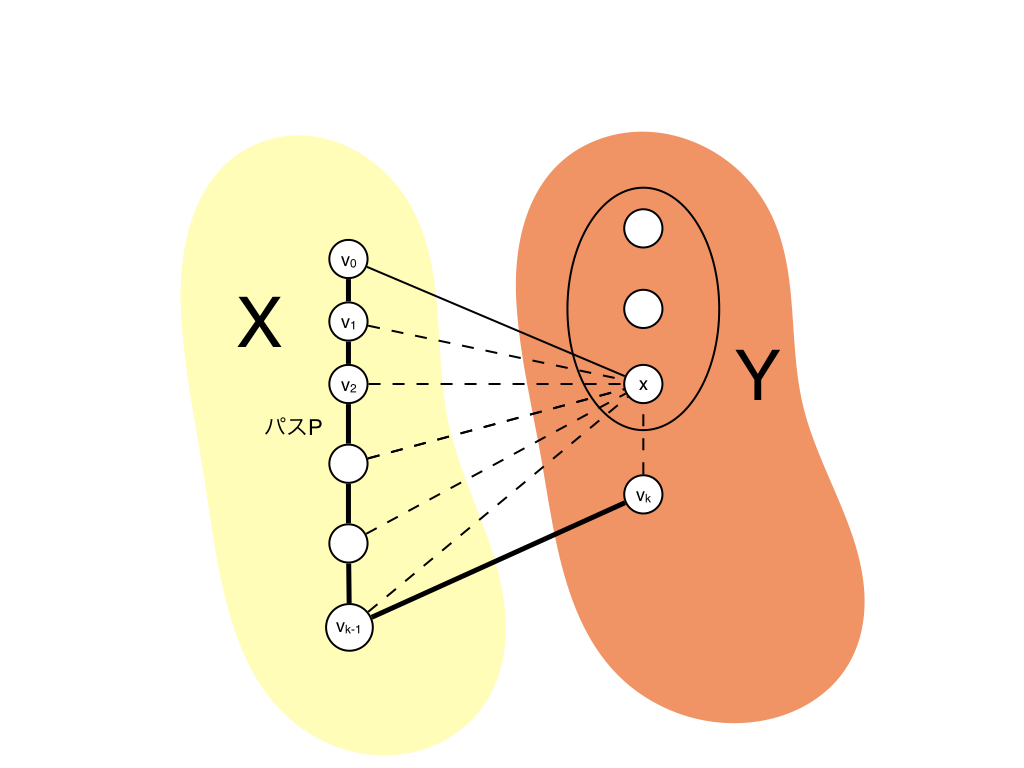
次に$N(v_0) \cap V_{id(v_0) + 1} \neq \emptyset$の場合を考えます． ここで，$x \in N(v_0) \cap V_{id(v_0) + 1}$とし， パス$P' = (x, v_0, \dots, v_k)$を考えます．$P$は$id(v_0)$が最大なchordless path， かつ$id(v_0) < id(x)$なので$P'$はchordを持つパスになります． $P$はchordless pathなので，$P'$の持つchordは$x$と隣接した辺になります． このときもつchordを$e = \set{x, y}$とすると， パス$P'' = (x, y = v_r, \dots, v_k)$が存在するのですが，これも$id(v_0)$の最大性より chordを持つパスになります．さらに，サイクル$C = (x, v_0, \dots, v_r = y, x)$を考えると， $G$がchordalであるという条件から$C$もchordを持ちます． このように，$x$を含むパスやサイクルはchordを持つため， どんどん短いパスやサイクルに分割ができます． この分割を繰り返すと，$P$中のすべての頂点は$x$と辺を持つことがわかります． （下の図のようになります．） つまり，$v_{k - 1}$は$x$と隣接します．したがって，$N(v_0) \cap V{id(v_0) + 1}$中の 任意の頂点は$v_{k - 1}$と隣接します．さらに， $v_0$は$P$がchordless pathであることから$v_k$と隣接せず， $v_{k - 1}$は$v_k$と隣接するので，$(2)$が証明できました． したがって，$G$がchordalの場合，$\alpha$は長さ2以上のchordless pathを持ちません． つまり，MCS順序はPEOになります． サイクルやパスで$P$が短くなっていくのは下の図のようになっています． 太線が$id(v_0)$が最大の誘導パス$P$を表し， 点線は$P$の$id(v_0)$の最大性と$G$がchordalであることから 存在することが証明できる辺です．

終わりに

これで，グラフがchordal graphかどうかを確かめる問題が線形時間で解けることがわかりました． 正当性の証明はそこそこ重い内容でしたが，とりあえず動きを知りたいという人にとっては MCSのアルゴリズム自体は簡単めかと思います．

余談ですが，今回のような「このグラフってhogehoge graphなの？」というYes/No問題のことをgraph recognitionと言います． なので，chordal graphのgraph recognitionは線形時間で解けるということですね！ あとはchordal graphってhyper graphのacyclic性を表すグラフクラスだとか，そういう話を 聞くのですが，ちゃんとはわかっていないので，気になっているところです．（気が向いたら勉強してブログに書くかも？）

次回はclicque treeについてお話ししようと思いましたが，Lex BFSが今回の内容に入らなかったので，先にそちらを説明します． clique treeは今までで一番面白い内容だと思うだけに先延ばしになってしまい残念... 今回から少しずつ内容が重くなっていくと思いますが，頑張ってわかりやすく書きたいと思うので，何かわからないことがあったら是非質問してください！